Зміст:
1.Комплексні числа
2.Кватерніони
3.Бікватерніони
4.Перетворення Лоренца
5.Перетворення Галілея
6.Релятивістські рівняння руху
7.Ефір як середовище, у якому розповсюджуються електромагнітні хвилі
8.Чи заперечують досліди Майкельсона і Морлі існування ефіру?
9.Рівняння Максвела.
1.Комплексні
числа
Дійсне число є основним і
найпростішим об`єктом
математики. Дійсні числа можна додавати, віднімати, множити і ділити. Ці дії
мають такі властивості:
комутативність
додавання (віднімання)
a + b = b +
a;
асоціативність
додавання (віднімання)
a + (b + c) = (a + b) + c;
комутативність
множення (ділення)
a
b
= b
a;
асоціативність множення (ділення)
a (b c) = (a b) c;
нарешті
зв`язок між множенням
і додаванням – закон дистрибутивності
a (b + c) = a
b
+ a c.
Крім зазначених вище операцій над
дійсними числами визначена ще операція взяття модуля дійсного числа, тобто
відкидання знаку мінус перед дійсним числом, якщо він там є. При цьому ця
операція має наступну властивість
│a b│ =
│a│ │b│.
Виникає
запитання: чи можна, наприклад, з двох дійсних чисел побудувати такий
математичний об`єкт,
над яким можна виконувати ті ж дії, що і над дійсними числами з тими самими їх властивостями?
Відповідь ствердна. Найпростішим таким об`єктом,
що визначається двома дійсними числами є комплексне число. Його можна задати
багатьма способами. Найпростіший з них – це задати комплексне число квадратною
матрицею другого порядку
z = (a, - b; b, a).
Тут
z
– комплексне число, a,
b
– дійсні числа. Матрицю нам
зручно записувати у один рядок, розділяючи елементи одного рядка комами, а
різні рядки комою з точкою. a
називається дійсною частиною комплексного числа a = Re(z), b називається
уявною частиною комплексного числа b
= Im(z).
Простота цього об`єкту
полягає у тому, що арифметичні дії над дійсними числами мають відповідні
аналоги для квадратних матриць другого порядку. Перевіримо
комутативність додавання (віднімання) матриць
z + z` = (a, - b; b, a) + (a`, - b`; b`, a`) = (a + a`, - b – b`; b – b`, a – a`) =
= (a` + a, - b` – b; b` – b, a` – a) = z` + z.
Комутативність
додавання є. Аналогічно перевіряємо асоціативність додавання (віднімання)
z + (z` + z``)=
= (a, - b; b, a) + [(a`, - b`; b`, a`) + (a``, - b``; b``, a``)] =
= (a, - b; b, a) + (a` + a``, – b` - b``; – b` - b``, – a` - a``) =
= (a + a` + a``, - b – b` - b``; - b – b` - b``, a –
a` - a``) =
= (a + a`, – b - b`; – b - b`, – a - a`) + (a``, - b``; b``, a``) =
= (z + z`) + z``.
Асоціативність додавання теж є. Перевіримо комутативність множення
z
z`
= (a,
- b;
b,
a) (a`, - b`; b`,
a`) = (a a` - b b`, - a` b – a b`; a` b + a b`, a a` – b b`) =
= (a` a – b` b, - a b` – a` b; a b` + a` b, a` a – b` b) =
= (a`, - b`;
b`, a`) (a, - b; b, a) = z` z.
Аналогічним
чином перевіряються і інші властивості цих операцій.
Тепер розглянемо ділення. Нагадаємо,
що для матриць діленню відповідає множення на матрицю, обернену дільнику. Для
матриці z` оберненою матрицею буде матриця
z`-1
= (a`, b`; - b`, a`) / (a`2 + b`2),
а
розв`язок відповідного рівняння можна записати так
z = z`` /
z` = z`` z`-1.
Тобто ділення – це також при матричному представленні комплексних чисел стандартна матрична дія. Матричне представлення комплексних чисел видається нам найбільш природним, оскільки не вимагає використання жодних операцій, крім тих, що добре визначені для матриць. Проте у нього є і недолік. Він полягає у надмірній громіздкості всіх викладок, пов`язаних з комплексними числами.
Ще однією формою представлення
комплексних чисел є векторна форма. Тут кожному комплексному числу ставиться у відповідність
вектор-стовпець з двома компонентами. Перша з них називається дійсною частиною
комплексного числа, друга – уявною. Вектор-рядок ми позначимо
z = (a, b),
вектор-стовпець
z = (a; b).
Складність
тут полягає у тому, щоб операцію множення векторів означити так, щоб вона мала
всі ті властивості, які існують для дійсних чисел і для комплексних чисел у
матричному представленні. Для векторів існують дві операції множення: скалярний
добуток і векторний добуток. Яку б з цих операцій ми не використали для
множення комплексних чисел у векторному представленні, її властивості не будуть
аналогічними операції множення дійсних чисел. Вихід полягає в об`єднанні цих двох операцій множення в одну,
а саме
z z` = ((z z`); [z z`]).
Тут
круглі дужки означають скалярний добуток двох векторів, квадратні – двовимірний
аналог векторного добутку. Іншими словами – це визначник, першим рядком
якого є числа a, b, другим рядком числа a`,b`
(z z`) = (a, b) (a`, b`) = a a` + b b`,
[z z`] = [(a, b) (a`, b`)] = a b` - a` b.
За
такого визначення добутку квадрат комплексного числа буде дійсною додатною
величиною
z z = ((z z); [z z]) = (a2 + b2; 0) =
(a2 + b2) (1; 0).
Розглянемо
тепер ділення комплексних чисел у векторному представленні. Нагадаємо, що у
будь-якому варіанті представлення комплексних чисел мова йде про розв`язок
рівняння
z z`= z``.
Тут чинитимемо аналогічно попередньому випадку. Домножимо обидві частини рівняння на z`
z z` z`= z`` z`
або
z (a2 + b2) (1; 0) =
z``
z`.
Розглянемо
тепер добуток, який позначимо як z*
z (1; 0) = (a; b) (1; 0) = (a; - b) = z*.
Відповідно,
z`` z` = ((z`` z`); [z`` z`]) = (a`` a` + b`` b`; a` b - a b`).
Остаточно,
z* = (a; - b) = (a`` a` + b`` b`; a` b + a b`)
/ (a`2 + b`2).
Дійсна
та уявна частини частки будуть такими
Re(z) = a = (a`` a` + b`` b`) / (a`2 + b`2),
Im(z) = b = - Im(z*) = (a`` b`- a` b``)
/ (a`2 + b`2).
Перевіримо
тепер виконання співвідношення для модулів. Для цього знайдемо квадрати
наступних комплексних чисел. При
цьому
множення комплексних чисел розумітимемо відповідно до введеного вище
z2 = (a; b) (a; b) = (a2 + b2) (1; 0),
z`2 = (a`; b`) (a`; b`) = (a`2 +
b`2) (1; 0),
z z` = (a a + b b`; a b` - a` b),
(z z`)2 = (a a + b b`; a b` - a` b) = [(a a
+ b b`)2 + (a b` - a` b)2] (1; 0) =
= (a2 + b2) (a`2 + b`2) (1; 0)
= z2 z`2.
Тут
ми скористались тим, що (1; 0)2 = (1; 0). Якщо модуль комплексного
числа у векторному представленні означити як
│z│ = (z2)1/2,
то
ми і отримаємо шукану рівність
│z z`│ = │z││z`│.
Векторне представлення комплексних
чисел є компактнішим з аналітичної точки зору і має просту геометричну
інтерпретацію. Кожному комплексному числу відповідає радіус-вектор. У висліді
кожній дій над комплексними числами відповідає наочний геометричний аналог.
Розплатою за цю простоту векторної форми представлення комплексних чисел є
складність операцій їх множення і ділення.
Комплексні числа утворюють алгебру.
Тобто комплексні числа утворюють векторний прості з операцією множення
елементів – комплексних чисел. Наявність операції множення означає, що добуток
двох комплексних чисел є комплексним числом. Отже множина комплексних чисел
замкнена щодо операції множення. Векторний простір за умовчанням означає, що
для його елементів – векторів (комплексних чисел) задані операції додавання і
множення на число – скаляр. Всі ці операції узгоджені між собою за допомогою
властивостей, які ми розглянули вище для комплексних чисел. Факт приналежності
комплексних чисел до алгебри робить можливим їх представлення у особливо
простій формі. Ця форма так і називається алгебраїчною. Вона полягає у запису
комплексного числа у вигляді простого алгебраїчного виразу
z = a + i b.
Платою
за простоту цієї форми представлення є присутність у виразі об`єкта, який не є дійсним число. Нагадаємо,
що у матричній і векторній формах представлення комплексних чисел комплексні
числа записували лише за допомогою дійсних чисел. Дійсними були матричні
елементи та компоненти векторів. Тут властивості нового об`єкту, який називається уявною одиницею,
розкривається співвідношенням
i2 = -1.
Множення
комплексних чисел в алгебраїчній формі представлення аналогічне множенню
алгебраїчних двочленів
z z` = (a + i b) (a` + i b`) = a a` - b b` + i (a b` +
a` b),
де
ми врахували властивість уявної одиниці. Для того, щоб розглянути ділення
комплексних чисел, нам потрібно ввести над комплексними числами ще одну
операцію – операцію комплексного спряження
z* =
(a
+ i b)* = a – i b.
Тобто
операція комплексного спряження полягає у заміні знаку перед уявною частиною
комплексного числа на протилежний. Цю операцію можна застосовувати і до дійсних
чисел, але тут вона не має особливого сенсу, оскільки a = a*, b = b* тощо.
Важливість операції комплексного спряження полягає у тому, що добуток
комплексного числа на комплексно спряжене є числом дійсним. Дійсно,
z z* = (a + i b) (a - i b) = a2 + b2.
Тепер
можна ввести поняття модуля комплексного числа і переконатись шляхом простих
алгебраїчних перетворень, що
│z z*│ = [(a a` - b b`)2 + (a b` + a` b)2]1/2,
│z│ = (a2 + b2)1/2 , │z`│
= (a`2
+ b`2)1/2,
│z z`│ = │z││z`│.
Тепер
ми розглянемо ділення комплексних чисел. Виходитимемо з загального уявлення про
операцію ділення. Розділити комплексне число z`` на комплексне число z`, отримавши в результаті комплексне
число z,
- це знайти розв`язок рівняння
z z`= z``.
Для
цього помножимо обидва боки рівняння на z*
z z` z`*= z`` z`*.
Оскільки
z z` z`* = z (a`2 + b`2) = z (a`2 + b`2),
то розв`язок рівняння має вигляд
z = (z`` z`) / z` z`* = [a`` a`
+ b`` b` + i (a` b`` - a`` b`)] / (a`2 + b`2).
Дійсна
і уявна частини частки будуть такими
Re(z) = Re(z``/z`) = (a`` a` + b`` b`) / (a`2 + b`2),
Im(z) = Im(z``/z`) = (a` b`` - a`` b`) / (a`2
+ b`2).
Між
трьома, розглянутими вище формами представлення комплексних чисел легко
встановити прямий зв`язок.
Якщо взяти за основу алгебраїчну форму комплексного числа, то обравши у цьому
виразі для одиниці представлення вектором (1; 0), а для уявної одиниці –
вектором (0; 1), ми отримаємо векторну форму представлення комплексного числа
z = a + i b = a (1; 0) + b (0; 1) = (a; 0) + (0; b) =
(a; b).
Представивши
одиницю одиничною квадратною матрицею другого порядку (1, 0; 0, 1), а уявну
одиницю матрицею (0, -1; 1, 0), ми отримаємо матричну форму представлення
комплексного числа
z = a + i b = a (1, 0; 0, 1) + b (0, - 1; 0, 1) = (a, 0; 0, a) + (0, - b; 0,, b) = (a, - b; b, a).
Простота
математичних викладок над комплексними числами в алгебраїчній формі і пояснює
її найбільшу вживаність у сучасній математиці. Звичайно для аналітичних
викладок використовують алгебраїчну форму представлення комплексних чисел, а
для їх геометричної інтерпретації – векторну.
2.Кватерніони
Кватерніони придумав Вільям Ровен
Гамільтон (William Rowan Hamilton) — ірландський математик і
фізик. Дата відкриття: 16 жовтня 1843 року. Він
буквально вигравірував формулу кватерніонів на мосту Брум у Дубліні,
коли йшов зі своєю дружиною — такий був момент натхнення! Цікаво, що поняття
вектора він ввів пізніше за поняття кватерніона.
В
математиці існує ще один об`єкт, властивості якого подібні до дійсних і комплексних чисел. Цей об`єкт називається кватерніоном. Кватерніони
задається четвіркою дійсних чисел. Він також є елементом векторного
простору, який називається кватерніонним, а отже для кватерніонів задані
операції додавання (віднімання) і множення на число – скаляр. Для кватерніонів
також визначена операція множення така, що добуток двох кватерніонів також є
кватерніоном. Тобто кватерніони утворюють алгебру. Єдина відмінність цієї
алгебри від алгебри комплексних чисел у тому, що алгебра комплексних чисел
комутативна, мається на увазі операція множення, а алгебра кватерніонів
некомутативна. Аналогічно комплексним числам для кватерніонів існують
алгебраїчна, векторна і матрична форми представлення. Матрична форма
представлення можлива як за допомогою квадратних матриць четвертого порядку з
дійсними матричними елементами, так і за допомогою матриць другого порядку, але
з комплексними матричними елементами. Розглянемо всі ці форми представлення
кватерніонів. Почнемо з алгебраїчної форми
q = a + b i + c j + d k.
Тут a, b, c, d –
дійсні числа, 1, i, j, k –
базисні елементи. В алгебраїчній формі i, j, k –
грають роль уявних одиниць, якщо порівнювати кватерніони і комплексні числа.
Між базисними елементами існують такі співвідношення
i2 = -1, j2 =
- 1, k2 = - 1,
i j = k, j k = i, k i = j,
j i = -
k, k j = - i, i k = -
j,
i j k = - k.
Це умови першого типу, що використовуються
також для базисних елементів. Існують і умови другого типу, які ми і будемо
використовувати надалі, якщо не буде зазначений інший варіант,
i2 = -1, j2 =
- 1, k2 = - 1,
i j = - k, j k = - i, k i = - j,
j i
= k, k j = i, i
k = j,
i j k = k.
Для компактності запису
кватерніонів для алгебраїчної форми традиційно використовують їх представлення
у вигляді суми скаляра і вектора
q = a + q.
Тут векторна частина кватерніона
q = b i + c j + d k,
Розглянемо два різні кватерніони
q1 = a1 + b1 i + c1 j + d1 k,
q2 = a2 +
b2 i + c2 j + d2 k.
Їхній добуток q = q1 q2 обчислюється для
умов першого типу за формулою
q = a1 a2 – (b1 b2 + c1 c2 + d1 d2) + a1 (b2 i + c2 j + d2 k) + a2 (b1 i
+ c1 j + d1 k) + (c1 d2 − d1 c2) i +
+ ( − b1 d2
+ d1 b2) j + ( b1 c2 − c1 b2) k.
Якщо використати скалярно-векторний
варіант алгебраїчної форми запису кватерніона, то добуток виглядатиме для умов
першого типу так
q = a1 a2 − (q1 q2)+ a1 q2 + a2 q1 + [q1 × q2].
Для умов другого роду
q = a1 a2 − (q1 q2)+ a1 q2 + a2 q1 - [q1 × q2].
Тут (q1 q2) – скалярний добуток векторних частин кватерніонів, що
реалізується за правилом скалярного множення векторів в евклідовому просторі,
але з протилежним знаком
(q1 q2) = - b1 b2 - c1 c2 - d1 d2,
[q1 × q2] – векторний добуток векторних
частин кватерніонів, що реалізується за правилом звичайного векторного множення
тривимірних векторів, тобто через обчислення наступного визначника
[q1 × q2] =
│i, j, k; b1, c1, c2, d1; b2, c2, d2│.
Тут
i, j, k - базисні елементи. Cкалярна частина добутку є
a
= a1 a2 − (q1 q2),
векторна
q = a1 q2 + a2 q1 + [q1 × q2]
або
q = a1 q2 + a2 q1 - [q1 × q2].
Саме
при такому доволі складному означенні добутку кватерніонів ця операція
задовольняє всім потрібним властивостям. Для кватерніонів вводиться додаткова
операція, якої немає для комплексних чисел, - операція кватерніонного
спряження. При операції спряження знак перед векторною частиною кватерніона
замінюється на протилежний. Спряжені
кватерніон ми позначатимемо великими літерами
Q = a – q.
Легко
переконатись, що добуток кватерніона на спряжений кватерніон є невід`ємним дійсним числом для умов обох типів
q Q = a2 + b2 + c2 + d2.
Така
властивість добутку кватерніонів дозволяє кожному з них поставити у
відповідність невід`ємне число – норму за найпростішим варіантом
N(x) = (q Q)1/2.
Тобто
норма – просто довжина чотиривімірного радіус-вектора, який можна поставити у
відповідність кватерніону. Для кватерніона вона завжди дійсна і суттєво невід`ємна.
Векторна частина кватерніона не випадково так
називається. Розглянемо два кватерніони без скалярної частини
q1 = b1 i + c1 j + d1 k,
q2 = b2 i + c2 j + d2 k.
Їх добуток визначатиметься так
q1 q2 =
− (q1 q2) - [q1 × q2].
Якщо q1 = q, а q2 = Q,
то [q1 × q2] = 0, а - (q Q) = b2 + c2 + d2
Якщо замість даних
кватерніонів розглянути тривимірні вектори з тими ж самими координатами, для
відміни від кватерніонів вектори ми позначимо їх великими літерами,
Q1 = b1 i + c1 j + d1 k,
Q2 = b2 i + c2 j + d2 k,
то їх скалярний і векторний добутки
визначатимуться так
(Q1 Q2)
= b1 b2 + c1 c2 + d1 d2,
[Q1 × Q2] =│і, j, k; b1, c1, c2, d1; b2, c2, d2│.
Тут і, j, k – одиничні орти
тривимірної декартової системи координат. Якщо Q1 = Q і Q2 = Q,
то [Q1 × Q2] =
0, а (Q Q) = b2 + c2 + d2. Тобто
скалярні добутки кватерніонів і векторів збігаються. Відмінність кватерніонних
одиниць від векторних ортів компенсується множенням кватерніона на спряжений кватерніон
у то час як вектор множиться сам на себе. У висліді норми векторів і
кватерніонів збігаються. Якщо ж розглядати векторний добуток, то він виглядає
формально однаковим і для кватерініонів і для векторів з можливою відміною у
знаку.
У
векторному представленні кватерніону можна поставити у відповідність
вектор-стовпець
q = (a; b; c; d).
Так само, як і у разі векторного
представлення комплексних чисел, ця форма представлення є незручною для
аналітичних викладок, але дуже зручною в якості геометричної інтерпретації
кватерніонів як векторів у чотиривимірному просторі. Операції над такими
векторами ми не будемо розглядати через їх складність. Від алгебраїчної форми
представлення кватерніонів можна легко перейти до векторної форми, якщо в
якості базисних кватерніонів взяти наступні
1 = (1; 0; 0; 0), b =
(0; 1; 0; 0), c =
(0; 0; 1; 0), d =
(0; 0; 0; 1).
До матричного представлення кватерніонів
квадратними матрицями четвертого порядку можна прийти, якщо для базисних
векторів кватерніона взяти такі матриці
1 = (1, 0, 0, 0; 0,
1, 0, 0; 0, 0, 1, 0; 0, 0, 0, 1),
i = (0, 0, 0, 1; 0, 0, -1, 0; 0, 1,
0, 0; -1, 0, 0, 0),
j = (0, 0, 1, 0; 0, 0, 0, 1; -1, 0,
0, 0; 0, -1, 0, 0),
k = (0, -1, 0, 0; 1, 0, 0, 0; 0, 0,
0, 1; 0, 0, -1, 0).
Легко переконатись, що для так означених
базисних елементів задовольняються всі наведені вище їх властивості. Нагадаємо,
що матричні елементи у рядку відділяються комами, а рядки – комою з точкою. У
матричному представленні дії над кватерніонами є відомими діями над матрицями.
Діленню кватерніонів відповідає множення кватерніона у чисельнику на
кватерніон, обернений знаменнику.
При використанні
алгебраїчної форми запису кватерніона вводиться поняття оберненого кватерніона
q-1 = Q / N2(q).
Тут Q – спряжений кватерніон, N2(q) - квадрат норми
кватерніона. У цьому разі при діленні кватерніона на кватерніон слід помножити
кватерніон у чисельнику на кватерніон обернений кватерніону у знаменнику.
На відміну від
комплексних чисел для кватерніонів існує два різних матричних представлення.
Одне, це за допомогою квадратних матриць четвертого порядку з дійсними
матричними елементами. Друге за допомогою квадратних матриць, але з
комплексними коефіцієнтами. Базисними елементами у цьому разі для умов першого
роду є наступні, де в якості матричних елементів для умов першого роду фігурують
уявні одиниці,
1 = (1, 0; 0,
1), i = iс (0, 1; 1, 0), j
= - iс (0, - iс; iс, 0), k
= iс (1, 0; 0, - 1),
для умов другого роду
1 = (1, 0; 0,
1), i = iс (0, 1; 1, 0), j
= iс (0, - iс; iс, 0), k
= iс (1, 0; 0, - 1),
Легко переконатись, що для
таких базисних елементів і умов першого типу виконуються всі їх властивості,
зокрема
i2 = (iс, 0; 0,
- iс) (iс, 0; 0, - iс) = - (1, 0; 0, 1),
j2 = (0, 1; -1, 0) (0, 1;
-1, 0) = - (1, 0; 0, 1),
k2 = (0, 1; -1, 0) (0, 1;
-1, 0) = - (1, 0; 0, 1),
i j = (iс, 0; 0, - iс)
(iс, 0; 0, - iс) = (0, iс; iс, 0) =
k,
або
i j = (iс, 0; 0, - iс)
(iс, 0; 0, - iс) = (0, iс; iс, 0) =
- k,
……………………………………………… .
Тут iс - уявна
одиниця для комплексних чисел. Довільний кватерніон тепер можна записати так
q = a (1, 0; 0, 1) + b iс
(0, 1; 1, 0) + - c iс (0, - iс; iс, 0)
+ d iс (1, 0; 0, - 1)
або
q = a (1, 0; 0, 1) + b iс
(0, 1; 1, 0) + c iс (0, - iс; iс, 0)
+ d iс (1, 0; 0, - 1).
Дані базисні кватерніони з точністю до множника iс або - iс збігаються з матрицями
Паулі.
σ1 = (0, 1; 1,
0), σ2 = (0,
- iс; iс,
0), σ3 = (1, 0; 0, -1),
які у лінійному просторі квадратних
матриць другого порядку утворюють повну ортогональну систему.
Якщо
в якості групової операції взяти операцію додавання кватерніонів, то вони
утворюють групу (адитивну) аналогічно дійсним і комплексним числам. Одиничним
елементом тут є нульовий кватерніон q0 = 0. Кожний
кватерніон q має обернений – q. Операція додавання для
кватерніонів є асоціативною. Оскільки операція додавання для кватерніонів є
також і комутативною то, така група називається комутативною або абелевою.
Нагадаємо, що сукупність будь-яких елементів утворює групу, якщо щодо групової
операції вона є замкнутою. Тобто результат цієї дії над двома елементами даної
множини є елементом цієї ж множини.
Якщо
в якості групової операції взяти операцію множення кватерніонів, то вони не утворюють
групу, оскільки один з них, а саме нульовий кватерніон, не має оберненого. Якщо
ж розглянути лише ненульові кватерніони, то вони утворюють мультиплікативну
групу, тобто групу щодо операції їх множення. Дійсно, добуток будь-яких
ненульових кватерніонів буде ненульовим кватерніоном. В якості одиничного
елемента групи можна взяти кватерніон q0 =
1. Для кожного ненульового кватерніона існує обернений. Множення кватерніонів
має властивість асоціативності. Ця група не комутативна, або не абелева.
Важливу
групу утворюють одиничні кватерніони щодо операції множення. Для таких
кватерніонів множення даного кватерніона на інший кватерніон означає його
поворот у тривимірному просторі на певний кут. Така група називається SU(2).
3.Бікватерніони
Бікватерніони (іноді їх називають бікомплексними
кватерніонами або комплексними кватерніонами) вперше
ввів Вільям Кінґдон Кліффорд (William Kingdon Clifford) у 1873
році.
Бікватерніони формально
визначаються аналогічно кватерніонам. Так їх алгебраїчна форма запису має
вигляд
q = a + b i + c j + d k.
Проте тут a, b, c, d –
комплексні числа, 1, i, j, k –
базисні елементи, які мають ті ж властивості, що і у разі
кватерніонів. Для бікватерніонів існує узагальнене поняття норми, але вона
може бути комплексним числом. На відміну від кватерніонів, норма яких дорівнює
нулю лише для нульових кватерніонів, ненульові бікватерніони можуть мати
нульову норму. Ділення бікватерніонів можливе лише, якщо дільник має ненульову
норму. Для бікватерніонів крім операції спряження – заміни знаку перед
векторною частиною на протилежний, існує операція комплексного спряження, яка
полягає у заміні знаку на протилежний перед уявною одиницею.
При
векторному і матричному представленні бікватерніонів базисні елементи такі ж як
і у кватерніонів, але коефіцієнти перед ними будуть вже комплексними. У разі
кватерніонів вони комплексні лише у разі представленні кватерніонів квадратними
матрицями другого порядку.
Бікватерніони
утворюють групу, якщо в якості групової операції взяти операцію додавання.
Дійсно, сума будь-яких бікватерніонів є бікватерніон. В якості одиничного
елемента можна взяти нульовий бікватерніон. Аналогічно кватерніонам, для
кожного бікватерніона існує обернений. Операція додавання бікватерніонів є
асоціативною. Оскільки вона є також комутативною, то така група називається
комутативною або абелевою.
Якщо
в якості групової операції взяти операцію множення, то групу утворюють лише
бікватерніони з ненульовою нормою. Тоді для кожного бікватерніона існує
обернений, в якості одиничного елемента можна взяти одиничний
бікватерніон q =1. Операція множення
асоціативна, але не комутативна. Тому дана група є не абелевою. Особливо
важливою для застувань групою є група бікватерніонів з одиничною нормою. Ця
група називається групою SL(2,C).
Кватерніони зручно
використовувати для ідентифікації точок у чотиривимірному просторі-часу.
Звичайно координати такої точки задають чотиривимірним вектором
(ct, x, y, z), де t -
час, x, y, z – просторові координати точки, c – швидкість світла. Кожній точці такого простору
можна поставити у відповідність кватерніон
q = c t + x i + y j + z k.
Тому такий простір називають кватерніонним. Тут i, j, k –
кватерніонні одиниці або базисні елементи. Також кожній точці чотиривимірного простору-часу
можна поставити у відповідність і бікватерніон
q = iс c t + x i + y j + z
k.
Квадрат норми бікватерніона має наступний
вигляд
│q │2= - c2 t2
+ x2 + y2 + z2.
Він може дорівнювати нулю і у разі, якщо
координати бікватерніона не дорівнюють нулю. Це відбувається тоді, коли дві
точки чотиривимірного простору-часу розташовані таким чином, що їх можна
поєднати світловим сигналом. Найпростіше це побачити, якщо розташувати їх на
одній з просторових осей координат, наприклад осі х. Тоді світловий сигнал,
відправлений з початку координат у момент t = 0, досягне точки з координатами (x, t) pа час t і пройде при цьому відстань x = c t
│q │2= - c2 t2
+ x2 = - c2 t2 + c2 t2 =
0.
Бікватерніон
q = c t + r = c t + x i + y j + z k є псевдоермітовим. Це означає, що одночасне
застосування до нього операцій спряження і комплексного спряження, яке
називається комбінованим спряженням, лише змінює його знак
Q* = -q.
Обертання бікватерніона у бікватерніонному
просторі здійснюється за допомогою подвійного бікватерніонного множення
q` =
s q S.
Тут s – одиничний бікватерніон
│s│= 1.
Якщо бікватерніон q є псевдоермітовим, то для псевдоермітовості бікватерніона q` бікватерніон s, який здійснює поворот, також має бути псевдоермітовим. Лише за цієї умови
симетрія бікватерніона q` при повороті
зберігатиметься. Ця умова дозволяє конкретизувати структуру бікватерніона s, а саме
s = iс σ + s.
Тоді
│s│2= - σ2
+ s2 = 1
4.Перетворення
Лоренца
Перетворення Лоренца були вперше запропоновані Гендріком Лоренцом у 1904 році в його статті: "Electromagnetic Phenomena in a System Moving with any Velocity less than that of Light" (англ. Електромагнітні явища в системі, що рухається з будь-якою швидкістю, меншою за швидкість світла. Але у 1895 році Лоренц вже використовував наближені варіанти цих перетворень (для малих швидкостей), вводячи поняття локального часу. У 1900 році він продовжив вдосконалювати ці ідеї. Лише в 1904 році він сформулював повні перетворення, які зберігають інваріантність рівнянь Максвелла.
Розглянемо дві інерціальні системи координат: S – нерухома система, S` - система, яка рухається вздовж осі x зі швидкістю v відносно системи S. Нехай у нерухомій чотиривимірній системі координат точка-подія має координати x, y, z, с t, а у рухомій системі координат та сама точка -подія має координати x`, y`, z`, с t`. Тут c – швидкість світла. Такий добуток нам потрібний для того, щоб всі координати чотиривимірного простору мали однакову розмірність, наприклад, просторових координат. Виникає запитання: координатами якого математичного об’єкта мають бути наведені нами координати? Тут слід взяти до уваги певну рівноправність просторових координат і часової координат, так само як і їх нерівноправність. Часова координата є виділеною. Спочатку розглянемо нерухому систему координат. У нас є декілька варіантів, але зупинимось на двох.
Перший - це координати кватерніона
s = c t + x i + y j + z k,
з нормою, що визначається добутком
кватерніона на спряжений кватерніон
N(s) = (s S)1/2 = {[c t + x i
+ y j + z k] [c t - x i - y j - z k]}1/2 =
= [c2 t2 + x2 +
y2 + z2]1/2,
де i, j, k – кватерніонні
уявні одиниці? Другий - це координати бікватерніона з тим же сенсом
величин i, j, k
q = ic c t 1
+ x i + y j + z k,
з нормою, що визначається добутком бікватерніона
на спряжений бікватерніон
N(s) = (q Q)1/2 = {[ic c t 1
+ x i + y j + z k] [ic c t 1
- x i - y j - z k]}1/2 =
= [- c2 t2 +
x2 + y2 + z2]1/2.
Припустимо, що у момент часу t =
0 початки координат K і K` збігаються і саме у цей момент
відбувається подія – вздовж додатного напрямку осі x відправляється
світловий сигнал нескінченно малої тривалості. Оскільки
x = x` =
0, y = y`=
0, z = z`=
0, t = t` = 0,
то і кватерніон, і бікватерніон дорівнюють
нулю. Якщо ж розглянути довільний момент часу, то і кватерніон, і бікватерніон будуть
відмінними від нуля. А норми? Якщо і кватерніон, і бікватерніон відповідають
світовому сигналу, що рухається як було зазначено вище, тобто точка
чотиривимірного простору-часу з координатами (r, t) пов`язана з початком координат виразом r = c t, то норми дорівнюватимуть нулю і у довільний момент
часу. А якщо розглянути рухому систему координат? Причому світловий сигнал
випромінюється у той момент, коли початки нерухомої і рухомої систем координат
збігаються, то кватерніон і бікватерніон та їх норми будуть такими
s` = c t` 1
+ x` i + y` j + z` k,
N(s`) = [c2 t`2 + x`2 + y`2 +
z`2]1/2,
q` = ic c t` 1
+ x` i + y` j + z` k,
N(q`) = [- c2 t`2 + x`2 +
y`2 + z`2]1/2.
Хоча кватерніон і бікватерніон у довільний
момент часу вже будуть ненульовими, їх норми, як було зазначено вище, нулю
дорівнюватимуть і надалі. Рівність квадратів норм кватерніонів і
бікватерніонів, що відповідають нерухомій і рухомій системам координат можна
записати так
c2 t2 + x2 +
y2 + z2 = c2 t`2 +
x`2 + y`2 + z`2,
- c2 t2 + x2 +
y2 + z2 = - c2 t`2 +
x`2 + y`2 + z`2.
Кватерніони і бікватерніони самою своєю природою враховують
зазначені вище особливості сукупності просторових координат і часу. Їх
нерівноправність полягає у тому, що часовій координаті відповідає скалярна частина
кватерніона і бікватерніона, а трьом просторовим координатам - векторна частина
кватерніона і бікватерніона. Разом з тим всі координати мають однакову
розмірність. Спроба використовувати векторні об`єкти, щоб поставити їх у
відповідність точкам чотиривимірного простору-часу з дивовижними властивостями
як векторів, так і самого простору-часу, виглядають не надто переконливими,
хоча доволі корисними для геометричної інтерпретації та аналітичних обчислень.
Ми
маємо дві різні рівності. Лише експеримент може підтвердити, яка з них
справедлива. А можливо обидві помилкові з експериментальної точки зору?
Перевірку почнемо з рівності для норм бікватерніонів у рухомій і нерухомій
системах координат. Зв`язок координат у рухомій і нерухомій системах координат
можна отримати багатьма способами. У цьому огляді ми розглянемо чотири. Перший
буде таким: шукатимемо лінійне перетворення між координатами обох інерційних
систем відліку
x` = a x + b t,
t` = d x + e t.
Оскільки рухома система відліку рухається
вздовж осі х нерухомої системи відліку, то інші просторові координати не
змінюються. Оскільки простір вважається однорідним та ізотропним, то
коефіцієнти цього перетворення є сталими величинами, що можуть залежати лише
від відносної швидкості руху систем відліку і швидкості світла. Розглянемо
світловий сигнал, що рухається у додатному напрямку осі х нерухомої системи
координат. Якщо це світловий імпульс нескінченно малої у часі протяжності, то
можна говорити про його координат, яка змінюється за законом
x = c t.
У рухомій системі координат його
координата змінюватиметься за законом
x` = c t`.
Підставимо вираз x = c t у
виписану вище систему рівнянь. Вона набере вигляду
x` = a c t + b t =
(a c + b) t,
t` = d c t + e t = (d c + e) t.
Тепер підставимо обидва вирази у
вираз x` = c t`
a c + b = c (d c + e).
Ми отримали рівняння, що пов`язує між собою
чотири коефіцієнти лінійного перетворення. Ще одне рівняння, що пов`язує між
собою ці ж чотири коефіцієнти, можна отримати, розглядаючи рух світлового
імпульсу у протилежному напрямку. У цьому разі
x = - c t.
У рухомій системі координат його
координата змінюватиметься за законом
x` = - c t`.
Закон перетворення координати і
часу буде тим самим
x` = a x + b t,
t` = d x + e t.
Підставимо вираз x =
- c t у виписану вище систему рівнянь. Вона набере вигляду
x` = - a c t + b t =
(- a c + b) t,
t` = - d c t + e t = (- d c
+ e) t.
Тепер підставимо обидва вирази у
вираз x` = - c t`
- a c + b = c (d c – e).
Отриману систему рівнянь можна спростити,
якщо розглянути їх суму і різницю
b = c2 d,
a = e.
Вихідну систему рівнянь, що визначає закон
перетворення від нерухомої до рухомої системи координат, тепер можна записати
так
x` = a x + c2 d t,
t` = d x + a t.
Подальше спрощення рівнянь можна отримати,
якщо використати той факт, що за дуже малої швидкості рух рухомої системи
координат щодо нерухомої зв`язок між просторовими координатами визначатиметься формулою Галілея
x = x`
+ v t,
x` = x + v t.
Припустимо, що і при великих швидкостях
він матиме подібний вигляд
x` = γ (x - v t),
де γ залежить лише від модуля швидкості
відносного руху систем відліку. Якщо ця швидкість прямує до нуля, то γ прямує
до одиниці і ми отримуємо перетворення Галілея. Це припущення відразу спрощує
задачу, оскільки
γ (x - v t)
= a x + c2 d t.
Остання рівність можлива лише тоді, коли
a = γ, d =
- γ v/ c2.
Тепер система рівнянь, що визначає закон
переходу між рухомою і нерухомою системами відліку матиме вигляд
x` = γ (x - v t),
t` = γ (t - x v / c2).
Використаємо тепер основне рівняння релятивістської
фізики – рівність квадратів норм бікватерніонів у рухомій і нерухомій системах
координат
- c2 t2 +
x2 + y2 + z2 = - c2 t`2 +
x`2 + y`2 + z`2.
Підклавши сюди x`, t`, отримаємо
- c2 t2 + x2 =
- c2 γ2 [t - (v / c2) x]2 +
γ2 [x - v t]2
γ2 x2 [1 -
(v / c)2] + γ2 t2 [- c2 + v2]=
- c2 t2 + x2.
Прирівнюючи коефіцієнти при однакових
координатах, отримуємо
γ = 1 / [1 - (v / c)2]1/2.
Остаточно перехід між нерухомою і рухомою
системами координат можна записати у вигляді
x` =
(x - v t) / [1 - (v / c)2]1/2,
t` = (t – x v / c2)
/ [1 – (v / c)2]1/2.
Ці перетворення називаються перетвореннями
Лоренца. Суть релятивістської фізики полягає у тому, що всі її рівняння мають
бути інваріантними щодо перетворень Лоренца, тобто мати один і той же вигляд у
будь-якій інерційній системі координат.
З
формул перетворень Лоренца випливає, що швидкість матеріального об`єкта не може перевищувати
швидкість світла, оскільки у цьому разі координати і час стають уявними. Цей
факт на сьогодні цілком узгоджується з відомими експериментальними даними. Ще
один висновок полягає у тому, що плин часу у різних інерційних системах
координат різний.
Виведемо ці формули
перетворення у ще один спосіб на основі простих геометричних міркувань. Нехай
вектор r з координатами (x, y) знаходиться у першій
чверті плоскої декартової системи координат. Кут між ним і віссю х дорівнює θ.
Тоді його проекції на осі координат будуть такими
x` = r
cos(θ), y` = r sin(θ).
Розглянемо тепер систему координат (x, y), що має спільний центр з системою координат (x`, y`), але повернута проти годинникової
стрілки довкола початку координат на кут φ. Координати вектора у штрихованій
системі координат будуть такими
x = r cos(θ - φ),
y = r sin(θ - φ).
Останні вирази можна записати і так
x = r cos(θ) cos(φ) - r sin(θ) sin(φ) = x` cos(φ) – y` sin(φ),
y = r sin(θ) cos(φ) + r cos(θ) sin(φ) = x` sin(φ) + y` cos(φ).
Знайдемо зв`язок між кутом φ і штрихованими координатами. Ми можемо обрати
нештриховану систему координат довільним чином. Оберемо її так, щоб вектор r був перпендикулярним осі х. Тоді проекція вектора r на цю вісь дорівнюватиме нулю. Зв`язок між нештрихованими
і штрихованими координатами тепер буде таким
x = - y sin(φ),
y = y cos(φ).
Розділивши перше рівняння на друге,
отримаємо
tan(φ) = - x / y.
Тепер перейдемо від вектора в двовимірному
евклідовому просторі до бікватерніона,
дві просторові координати якого дорівнюють нулю. Руху цієї системи координат
вздовж додатного напрямку осі х нерухомої системи координат відповідає поворот
бікватерніона у бікватерніонному просторі на кут φ. При цьому координат
бікватерніона змінюються за законом: x` = V t`, y` = ic c t`. Такі формули
визначають штриховану систему координат як таку, що рухається щодо нештрихованої
системи координат з швидкістю V. Тоді
tan(φ) = - V t / (ic
c t) = ic V / c.
Тобто тангенс кута повороту бікватерніона
прямо пропорційний швидкості руху однієї інерційної системи координат щодо
іншої. Оскільки
cos(φ) = 1 / [1 + tan2(φ)]1/2 = 1 / (1 - V2 / c2)1/2,
sin(φ) = cos(φ) tan(φ) = ic
(V / c) / (1 - V2 / c2)1/2,
то ми отримуємо
перетворення Лоренца
x = (x` + V t`) / (1 - V2 / c2)1/2,
t = (t` + V x` / c2) / (1 - V2 / c2)1/2.
Нарешті, знайдемо
перетворення Лоренца у загальному вигляді, використовуючи бікватерніонну
алгебру. Тут слід звернути увагу на той факто, що бікватерніон, який відповідає
просторовим координатам і часу має певну симетрію. Він є псевдоевклідовим,
тобто якщо виконати кватерніонне і комплексне спряження одночасно, то ми
отримаємо вихідний бікватерніон з протилежним знаком
Q* = (iс c t - r)* = - (iс c t - r) = - q.
Для того, щоб при повороті бікватерніона
його симетрія не змінилась, спеціальний бікватерніон також повинен мати
аналогічну симетрію. Це можливо лише у разі, якщо
s = (iс σ + s).
При цьому квадрат його норми має
дорівнювати одиниці. Якщо відповідний добуток ми розглянемо за правилами
добутку бікватерніонів, то
s S = (iс σ + s) (iс σ - s) = - σ2 + s2 = - σ2 + sx2 + sy2 + sz2 = 1.
Тут s2 – це квадрат вектора s2 = sx2 + sy2 + sz2. Якщо відповідний добуток
розглянути як добуток двох алгебраїчних виразів, то
s S = (iс σ + s) (iс σ - s) = - σ2 - s2 = - σ2 + sx2 + sy2 + sz2 = 1.
Тут s2 – це квадрат векторної
частини бікватерніона s2 = -
sx2 - sy2 - sz2. В
обох підходах результати тотожні. Спеціальний кватерніон s має ту властивість, що якщо швидкість, з якою рухома
інерційна система відліку рухається щодо нерухомої системи відліку прямує до
нуля, то s прямує до одиниці.
Перетворення Лоренца
бікватерніона можна подати як подвійне кватерніонне множення відповідного
бікватерніона
q` = - s q S* = s q
s.
Такий подвійний бікватерніонний добуток
дійсно реалізує поворот бікватерніона у бікватерніонному просторі при
незмінному його модулі. Якщо відносна швидкість двох інерційних систем відліку
прямує до нуля, то бікватерніон q` прямує до бікватерніона q. Якщо бікватерніон, що обертається не є псевдоермітовим, то його обертання здійснюється за загальним правилом. При обертанні
кватерніона в площині x0t спеціальний кватерніон має вигляд s = iс σ + i sx, у площині
y0t - s = iс σ +і sy , у площині
z0t спеціальний кватерніон має вигляд s = iс σ + i sz. Знайдемо загальну
структуру такого перетворення для бікватерніона, координатами якого є
просторові координати і час. Здійснимо довільний оберт довкола початку
координат. Оскільки
s q = - σ c t – (s r)
+ iс (σ r + c t s) –
[s × r].
Відповідно,
q` = - s q s+ = s q s
= {- σ c t – (s r) + iс (σ r + c t s) –
[s × r]} (iс σ + l) =
= - [{ - [s × r]
+ iс (σ r + c t s)} × s]
– σ c t s – (s r) s + iс σ
{- [s × r] + iс (σ r + c t s)} –
-{σ c t + (s r)} iс σ
– ({- [s × r] + iс (σ r + c t s)}
s)
Надалі скористаємось властивостями
змішаного скалярно-векторного добутку
[s × r] s =
[s × s] r =
0
та подвійного векторного добутку
[[s × r]
× s] = s (s r) – r s2 – 2 σ c t s
Тепер
q` = r (s2 -σ2) –
2 (s r) s – 2 σ c
t s - iс c t s2 - iс σ2 c t
-2 iс σ (s r) =
= r (s2 -σ2) –
2 (s r) s – 2 σ c
t s+ iс c t s2 – 2 iс c t s2 - iс σ2 c t
-2 iс σ (s r) =
= r (s2 -σ2) –
2 (s r) s – 2 σ c
t s + iс {c t (s2 - σ2)
– 2 c t s2 -2 σ (s r)} =
= r –
2 (s r) s – 2 σ c
t s + iс {c t – 2 c t s2 -2
σ (s r)}.
Легко перевірити, що норма бікватерніона
при такому подвійному бікватерніонному множенні залишилась незмінною
│ q` │2 = q` Q` = q Q = - c2 t2 + r2 =│ q │2.
Якщо оберт здійснюється у площині х0t, то всі скалярні добутки векторів мають
розглядатись саме як для векторів, а не для векторних частин бікватерніонів, і формула
перетворення буде наступною
q` = iс {c t (1 – 2 sx2) -
2 σ sx x} + {x (1 – 2 sx2) – 2 σ sx
c t } i.
Тут норма визначатиметься подібним чином
│ q` │2 = q` Q` = q Q = - c2 t2 + x2 =│ q │2
Порівнюючи отриманий результат з отриманим
раніше
q` = iс (с t
– x v / c) / [1 – (v / c)2]1/2 + (x + v t) / [1
- (v / c)2]1/2 i,
отримаємо вирази для компонент одиничного
бікватерніона
1 – 2 sx2 =
γ = 1 / (1 – V2 / c2)1/2,
2 σ sx = - (V / c) / (1 – V2 / c2)1/2.
Розв`яжемо перше рівняння
щодо просторової компоненти одиничного бікватерніона
sx = iс [( γ - 1) /
2]1/2.
Використовуючи квадрат норми одиничного
бікватерінона можна переписати перше рівняння щодо скалярної частини одиничного
бікватерніона - σ2 + sx2 = 1
1 – 2 sx2
= 1 – 2 (1 + σ2) = - 1 - 2 σ2 =
γ.
Звідси
σ = iс [(γ
+ 1) / 2]1/2.
Друге рівняння можна використати для
перевірки правильності розв`язків
2 σ sx =
2 iс2 [(γ - 1) / 2]1/2 [(γ + 1)
/ 2]1/2 = - [(γ - 1)(γ + 1)]1/2 = - (V / c)
/ (1 – V2 / c2)1/2.
Недолік останнього виводу полягає у тому, що ми спочатку знайшли
перетворення Лоренца простішими методами, а потім використали отримані
результати для реалізації методики знаходження методами бікватерніонної
алгебри.
Нехай в одній просторовій точці нерухомої системи координат відбуваються дві події в різні моменти часу, тобто у нерухомій системі координат часова відстань між цими подіями буде
x2 = x1, t2 - t1.
Знайдемо цю ж відстань у рухомій системі
координат, яка також відбувається в одній просторовій точці але рухомої системи
координат,,
x2` = x1`, t2`
- t1`.
Відповідно до перетворень Лоренца цей зв`язок буде наступним
t2` - t1` = (t2 - t1)
/ [1 – (v / c)2]1/2
Якщо спостерігач знаходиться у нерухомій
системі координат, то проміж часу, який він спостерігатиме, буде наступним
t = t2` - t1` =
(t2 - t1) / [1 – (v / c)2]1/2 =
t0 / [1 – (v / c)2]1/2,
тобто він буде більшим, ніж показав би
годинник у рухомій системі координат. Якщо ж спостерігач знаходиться у рухомій
системі координат, то проміжок часу, який він спостерігатиме, буде меншим за
той, що показуватиме годинник у нерухомій системі координат
t = t2 - t1 =
(t2` - t1`) [1 – (v / c)2]1/2 =
t0 [1 – (v / c)2]1/2.
Тобто у нерухомій системі координат, щодо
якої спостерігач знаходиться у спокої, час тече швидше, ніж у рухомій системі
координат. Тобто у рухомій системі координат з точки зору спостерігача, що в
ній знаходиться, час тече повільніше, ніж у нерухомій системі координат. У
нерухомій системі координат, якщо спостерігач в ній знаходиться, час тече
швидше, ніж у рухомій системі координат. Ці формули були перевірені експериментально
через спостереження розпаду повільних і високошвидкісних мезонів і
підтвердились.
Запишемо тепер зв`язок просторового
інтервалу у рухомій і нерухомій системах координат. Очевидно, що
x2` - x1`
= (x2 - x1) / [1 – (v / c)2]1/2
Якщо спостерігач знаходиться у рухомій
системі координат і одновимірне, також нерухоме щодо цієї системи координат,
має довжину l0 = x2` - x1`,
то щодо нерухомої системи координат, щодо якої це одновимірне тіло рухається,
його довжина буде l = x2 - x1.
Видно, що
l = l0 [1
– (v / c)2]1/2.
Тобто у нерухомій системі координат, щодо
якої тіло рухається, довжина тіла буде менше, ніж у рухомій системі координат,
щодо якої тіло знаходиться у стані спокою.
Загальним
законом сучасної фізики є твердження, що всі основні рівняння сучасної фізики
мають бути інваріантними щодо перетворень Лоренца. однаковими у всіх інерційних
системах відліку. Вперше цю думку висловив Анрі Пуанкаре у серпні 1904
року на Всесвітньому конгресі в Сент-Луїсі (США), у виступі "Про
динаміку електрона", де прямо сказав: "Закони фізичних
явищ повинні бути однакові для спостерігача, що рухається рівномірно
прямолінійно, і для спостерігача в стані спокою." Пізніше це
твердження стало називатись принципом відносності, а релятивістську фізику
стали називати теорією відносності.
Розглянемо перетворення координат у разі кватерніонів. Весь розгляд буде аналогічним, за виключенням того, що квадрат норми кватерніона тепер буде іншим
c2 t2 + x2 + y2 + z2 = c2 t`2 + x`2 + y`2 + z`2.
Підклавши сюди x`, t`, отримаємо
c2 t2 + x2 = c2 γ2 [t –
(v / c2) x]2 + γ2 [x – v t]2
або
γ2 x2 [1 +
(v / c)2] + γ2 t2 [c2 + v2]= c2 t2 + x2.
Прирівнюючи коефіцієнти при відповідних
координат, отримуємо
γ = 1 / [1 + (v / c)2]1/2.
Тепер закон перетворення координат при
переході від нерухомої системи координат до рухомої буде таким
x` =
(x – v t) / [1 + (v / c)2]1/2,
t` = (t – x v / c2)
/ [1 + (v / c)2]1/2.
З цих формул перетворення випливає, що жодних обмежень на швидкість
світла немає, а всі релятивістські ефекти типу залежності довжини і проміжку
часу від вибору системи відліку мають прямо протилежний характер щодо ефектів,
що випливають з перетворень Лоренца. Отже ці перетворення не відповідають
наявним на сьогодні експериментальними даним.
Розглянемо
релятивістський закон додавання швидкостей. Нехай рухома система координат
рухається вздовж осі x з швидкістю V, а матеріальна точка у цій
рухомій системі координат рухається у тому ж напрямку з швидкістю v`.
Виникає запитання, з якою швидкістю ця матеріальна точка рухатиметься щодо
нерухомої системи координат? Для відповіді на це запитання розглянемо
перетворення Лоренца у диференційній формі
dx`
= (dx – V dt) / [1 + (V / c)2]1/2,
dy` = dy,
dz` = dz,
dt` = (dt – dx V / c2)
/ [1 + (V / c)2]1/2.
Ці формули краще переписати для
диференціалів координат нерухомої системи координат через диференціали
координат рухомої системи координат. Замінивши v на – v, отримаємо шукану
швидкість у нерухомій системі координат
dx = (dx` + V dt`) / [1
+ (V / c)2]1/2,
dy = dy`,
dz = dz`,
dt = (dt` + dx` V / c2)
/ [1 + (V / c)2]1/2.
Розділивши перші три рівняння на четверте,
і обмежившись для простоти випадком, коли y = y`
= const, z = z` = const, отримаємо
dx/dt = vx = (vx` + V) / (1
+ vx` V / c2).
Видно, що коли швидкість матеріальної
точки щодо рухомої системи координат наближається до швидкості світла, як і
швидкість самої рухомої системи координат, то її швидкість у нерухомій системі
координат також наближається до швидкості світла. Тобто сума двох швидкостей
світла є швидкістю світла, а не подвоєною швидкістю світлі. Якщо ж швидкість
матеріальної точки, так само як і швидкість рухомої системи координат щодо
нерухомої, є малою у порівнянні з швидкістю світла, то виконується звичайний
закон додавання швидкостей, коли результуюча швидкість є сумою складових.
5.Перетворення Галілея
Галілео Галілей (1564–1642) —
висловив основні ідеї інваріантності фізичних законів у різних інерційних
системах ще на початку 1600-х років. Формалізація перетворень Галілея (тобто
чітке математичне формулювання) з’явилася пізніше, в рамках класичної механіки Ісака
Ньютона (кінець XVII – початок XVIII ст.). Як розглянути дві інерційні системи
відліку нерухому S і рухому S`, причому
остання рухається щодо нерухомої системи відлуку із швидкістю V, то ці
перетворення мають виглядw, якщо осі
координат обох систем паралельні, швидкість паралельна осі x нерухомої
системи і спрямована у її додатному напрямку,
x(t)= x`(t`) + V t
Це перетворення має доволі простий фізичний зміст.
Координата матеріальної точки у нерухомій системі відліку буде дорівнювати сумі
координати цієї матеріальної точки у рухомій системі відліку з додаванням
відстані, що пройде за час спостереження t.це рівняння
можна переписати і так
x`(t`)= x(t) - V t.
При цьому час в обох системах відліку тече однаково,
тобто
t = t`.
Легко бачити, що рівняння другого закону Ньютона
інваріантне щодо цього перетворення. Запишемо його у рухомій системі відліку для одновимірного
випадку
m (d2x`(t`)/dt`2) = F(x`).
Тут m – маса
матеріальної точки, F(x`) – сила, що діє на неї. Перейдемо до нерухомої системи відліку
dx`(t`)/dt` = d[x(t) + V t]/dt = dx(t)/dt + V,
d2x`(t`)/dt`2
= d/dt [dx(t)/dt + V] = d2x(t)/dt2.
Отже, у нерухомій системі координат другий закон
Ньютона матиме той же вигляд
m (d2x(t)/dt2) = F(x).
q Можна
показати, що рівняння Максвела, які описують електромагнітні явища, не
інваріантні щодо перетворень Галілея. Принциповим моментом перетворень Галілея
було твердження, що плин часу в обох системах відліку – рухомій і нерухомій
однаковий. Рівняння фізики, інваріантні щодо перетворень Галілея доволі точно
описують фізичні явища при швидкостях, малих щодо швидкості світла c.Але навіть
при малих швидкостях перетворення
Галілея можна уточнити, відмовившись від останнього твердження. Для цього
розділи перший закон перетворення на швидкість світла
x(t)/c = x`(t`)/c + (V/c) t.
Якщо уявити собі ситуацію, коли в початковий момент
часу початки нерухомої і рухомої систем відліку збігались, і у цей момент був
випущений світловий сигнал у напрямку руху рухомої системи відліку, то x(t)/c = t – це час, за
який цей сигнал у нерухомій системі координат пройде відстань x(t). Відповідно,
x`(t`)/c = t` - це час,
за який цей сигнал у рухомій системі координат пройде відстань x`(t`). Тепер
можна це рівняння записати як рівняння для часі, що показують годинники у
нерухомій і рухомій системах координат
t = t` + (V/c) t.
Тобто час у нерухомій системі координат, зa який
світловий сигнал пройде відстань x = c t, дорівнює
сумі часів за який сигнал дійде до цієї ж точки простору у рухомій системі
координат x` = c t` i часу, за
який початок системи координат пройде відстань V t. Тут вже
плин часу у нерухомій і рухомій системах координат відрізняються. Ясно, що час t` менший за
час t, оскільки у
рухомій системі координат світловому сигналу потрібно пройти меншу відстань
через те, що у тому ж напрямку рухається і початок координат. Остаточно
t` = t + (V/c) [x(t)/c].
Можна
припустити, що у рухомій системі координат швидкість світла буде іншою, ніж у
нерухомій системі координат, а плин часу такий як і у нерухомій системі
координат. Позначимо швидкість світла у рухомій системі координат через c`. Тоді
закон руху світлового сигналу у рухомій системі координат буде x = c` t. Підклавши
цей вираз у вихідне рівняння, x(t)= x`(t`) + V t, отримаємо
c t = c` t +
V t
або
c` = c – V.
Отже ми маємо альтернативу: або вважати, що плин часу
однаковий в обох системах відліку і тоді швидкість світла у рухомій системі
відліку менша за швидкість світла у нерухомій системі відліку на величину
швидкості рухомої системи відліку щодо нерухомої, або швидкість світла у
рухомій системі відліку така сама як і у нерухомій системі відліку, а плин часу
повільніший. Перший варіант нам не підходить, оскільки він збігається з
перетвореннями Галілея, а другий варіант дає можливість пошуку законів
перетворення, що були б справедливими і при великих швидкостях. Більше того,
другий варіант працює для швидкостей, для яких виконується умова V2/c2 << V/c. Для довільних швидкостей, але таких, що не перевищують швидкість
світла можна шукати точний закон перетворень у вигляді
x` = α
(x - v t),
t`
= β (t - x v / c2),
де коефіцієнти α і β залежать лише
від абсолютної величини швидкості V.
Оскільки
ми припустили, що світло в усіх системах відліку розповсюджується з тою самою
швидкістю c,
то квадрат норми кватерніона, що відповідає спостереженню імпульсу світла через
час t
у
нерухомій системі координат і час t`
у рухомій системі координат в одній і тій самій точці простору Мінковського, буде
тим самим, тобто
- c2 t2 + x2 + y2
+ z2 = - c2 t`2 + x`2 + y`2
+ z`2.
Підкладаючи сюди x` i t`
, отримаємо
c2 t2 + x2 = c2 β2 [t –
(v /
c2)
x]2
+ α2 [x
–
v t]2 .
Розкриваючи дужки і прирівнюючи
коефіцієнти при однакових координатах у лівій і праві частинах рівняння,
отримаємо
α2 = 1 / (1- V2/c2),
β2 = 1 / [c2 [t –
(v /
c2)].
Відповідно, отримуємо вже наведений
вище, результат
x`
= (x – v t) / [1 + (v /
c)2]1/2,
t`
= (t – x v / c2) / [1 + (v /
c)2]1/2.
Вперше релятивістська формула додавання швидкостей з`явилась в роботах Гендріка Лоренца, а пізніше і роботах Анрі Пуанкаре. Ця формула настільки прив`язана до перетворень Лоренца, що було б дивним, якби науковець, що запропонував світові формули перетворень, не запропонував би і закон додавання швидкостей у релятивістській формі.
6.Релятивістські рівняння руху
Знайдемо закон
перетворення швидкості і прискорення матеріальної точки, що рухається відносно
рухомої системи координат із швидкістю v вздовж осі x`. При цьому ця система
координат рухається із швидкістю V відносно нерухомої системи координат вздовж її осі x. Для цього запишемо перетворення Лоренца для диференціалів координат і
часу
dx` = (dx – V dt)
/ (1 – V2/c2)1/2,
dt` = (dt – V dx/c2)
/ (1 – V2/c2)1/2.
Розділивши перше рівняння на друге, отримаємо
закон перетворення для швидкості
v` =
(v – V) / (1 – v V/c2).
Аналогічно знайдемо і закон перетворення
прискорення
a` = dv`/dt` =
d[(v – V)/(1 – v V/c2)]/dt (dt/dt`) = a (1 – V2/c2)3/2/(1
– v V/c2)3.
Підставимо вираз для прискорення у
класичний варіант закону Ньютона
m a` = F`
або
[(1 – V2/c2)3/2
/ (1 – v V/c2)3] m a = F.
Ми бачимо, що форма другого закону Ньютона
при переході до нерухомої системи відліку не зберігається. Причина полягає у
тому, що ми здиференціювали бікватерніон, компонентами якого є координати і
час, за змінною, як сама залежить від вибору системи відліку. Цією змінною є
час t` у рухомій системі відліку. Така операція надто
ускладнює структуру бікватерніонів швидкості і прискорення і, відповідно,
рівняння руху. Хоча інваріантності можна досягти і тут, задавши відповідний
закон перетворення сили, але цей закон перетворення буде надто складним.
Отримані нами закони
перетворення для швидкості і прискорення описують наступний механічний рух:
матеріальна точка рухається довільним чином з швидкістю vx вздовж осі x` щодо рухомої системи відліку. При цьому ця система відліку сама рухається
з швидкістю V щодо нерухомої системи відліку. Відповідні вісі
координат обох систем паралельні. Така схема є занадто складною, що і
призводить до зайвого ускладнення формул перетворення для швидкості і
прискорення. Спростимо схему. Розглянемо рух матеріальної точки наступним
чином. Матеріальна точка знаходиться у стані спокою щодо певної системи відліку,
а сама ця система рухається з швидкістю vx щодо нерухомої системи відліку. Осі
координат обох систем паралельні, а позначення координат і часу в них
відрізняються штрихом, як і у попередньому випадку. Час t` у системі відліку, щодо
якої матеріальна точка нерухома, називається власним часом і він є скаляром. Час
t у нерухомій системі відліку пов`язаний з часом у системі
відліку, що рухається разом з матеріальною точкою, співвідношенням, отриманим
нами вище,
t` = t (1 – vx2 / c2)1/2.
Тут ми скористались формулою, отриманою
для переходу між інерційними системами відліку для випадку, коли одна система
відліку щодо іншої може рухатись з довільною і змінною у часі швидкістю.
Фактично ми припустили, що у будь-який нескіченно малий проміжок часу рухому
систему відліку можна вважати інерційною.
Якщо ми здиференціюємо
бікватерніон за власним часом матеріальної точки, тобто за скаляром, то ми
мінімально змінимо структуру бікватерніона швидкості щодо бікватерніона
координат і часу. Для матеріальної точки, нерухомої щодо певної системи
відліку, але яка рухається щодо нерухомої системи відліку із швидкістю vx перетворення Лоренца матимуть вигляд
x = x` / (1 – vx2 / c2)1/2,
c t = c t` / (1 – vx2 / c2)1/2.
Знайдемо відповідні похідні
ux = (dx/dt) (dt/dt`) = vx / (1 – vx2 /c 2)1/2,
ut = c dt/dt`
= c / (1 – vx2 / c2)1/2.
Бікватерніон швидкості тепер матиме вигляд
u = ic
ut + ux i = ic c / (1 – vx2 / c2)1/2
+ vx / (1 – vx2 / c2)1/2
i.
Якщо знайти норму бікватерніона швидкості,
то вона буде від`ємною
u U = - c2
/ (1 – vx2 / c2) + vx2 /
(1 – vx2 / c2) = - c2 < 0.
Така норма називається часоподібна. Аналогічно
знайдемо бікватерніон прискорення
wx = dux/dt` = d[vx / (1 – vx2 / c2)1/2] / dt` = ax / (1 - vx2 / c2)2,
wt = dut/dt` = d[vx / (1 – vx2 / c2)1/2] / dt` = ax (vx/c) / (1 - vx2 / c2)2.
Бікватерніон прискорення матиме вигляд
w = ic
wt + wx i = ic ax (vx / c) / (1 - vx2 / c2)2 + ax / (1 - vx2 / c2)2 i.
Якщо аналогічно знайти норму бікватерніона
прискорення, то вона завжди буде додатною. Така норма називається
простороподібною. Норма бікватерніона, що відповідає координатам і часу, може
мати будь-який знак.
Від швидкості матеріальної точки можна
перейти до її імпульсу, помноживши її на масу матеріальної точки
px = m0
ux = m0 vx / (1 – vx2 / c2)1/2,
pt = m0
ut = c dt/dt` = m0 c / (1 – vx2 / c2)1/2.
Вирази для координат імпульсу можна
переписати і у традиційній формі як добуток маси на швидкість, ввівши замість
маси спокою m0 масу матеріальної точки у стані руху із відповідною
швидкістю. Тоді від швидкості залежатиме маса матеріальної точки
m = m0 / (1 – vx2 / c2)1/2.
Відповідно
px = m ux,
pt = m ut.
Тепер можна записати рівняння руху. Їх
буде у даному разі два, відповідності до того, що змінюються в нашому
конкретному випадку лише дві координати бікватерніона – просторова координата x і час t
(dpx/dt) / (1 – vx2 / c2)1/2 = fx,
(dpt/dt)
/ (1 – vx2 / c2)1/2 = ft.
Першу рівняння відповідає другому закону
Ньютона, записаному у релятивістській формі, друге рівняння – закону збереження
енергії. Ці рівняння традиційно записують так
(dpx/dt)
= fx (1 – vx2 / c2)1/2,
(dpt/dt)
= ft (1 – vx2 / c2)1/2.
Бікватерніон сили тепер можна записати так
F = ic Ft
+ Fx і = ft (1 – vx2 / c2)1/2 + fx (1 – vx2 / c2)1/2 i.
Тепер координати бікватерніона сили також
залежать від швидкості і перше рівняння можна записати так
(dpx/dt) = Fx.
Видно, що при переході від системи
відліку, щодо якої матеріальна точка знаходиться у стані спокою, до нерухомої
системи координат, щодо якої ця точка рухається, форма рівняння зберігається. Якщо
швидкість матеріальної точки прямує до нуля, то це рівняння переходить у
класичне рівняння Ньютона, оскільки величина (1 – vx2/c2)1/2 прямує до одиниці, маса
матеріальної точки прямує до її маси спокою, імпульс до добутку маси спокою на
швидкість матеріальної точки, сила до її класичного значення.
Розглянемо
тепер друге рівняння. З`ясуємо сенс компоненти сили ft. Якщо здиференціювати квадрат норми
бікватерніона швидкості за власним часом, то отримаємо
d[- ut2 + ux2]
/ dt` = - 2 ut (dut/dt`) + 2 ux (dux/dt`)
= - 2 ut at + 2 ux ax = 0.
Це рівняння можна записати для сили у
системі координат, де матеріальна точка знаходиться у стані спокою
- ut m0
at + ux m0 ax = - ut ft
+ ux fx = 0.
Звідси можна знайти компоненту сили ft і виразити її через силу
у системі координат, щодо якої матеріальна точка рухається
ft = ux fx / ut = ux
Fx / [c (1 – vx2 / c2)1/2]
Друге рівняння тепер матиме вигляд
d[m0 c2/ (1 – vx2 / c2)1/2 ] / dt = ux Fx.
Оскільки у правій частині рівняння
міститься робота сили над матеріальною точкою за одиницю часу, то у лівій має
знаходитись зміна енергії E за одиницю часу. Отже,
E = m0 c2/ (1 – vx2/c2)1/2.
Вираз у чисельнику m0 c2 називають релятивістською енергією матеріальної точки. Першим цю формулу отримав Анрі
Пуанкаре у статті "La théorie de Lorentz et le principe de réaction" (1900).
Там він писав: “Випромінювання переносить імпульс, і щоб зберігався принцип дії
й протидії, треба припустити, що випромінювання має масу.” Він ввів "механічний
еквівалент енергії", кажучи, що випромінювання діє на тіло так, наче воно
має масу: m = E / c2. Альберт Айнштайн
запропонував цю формулу як універсальну, незалежну від природи матеріального об`єкта.
7.Ефір як середовище, у якому розповсюджуються електромагнітні хвилі
Джеймс Клерк Максвелл (1831 - 1879) видатний шотландський фізик
Джеймс Клерк Максвел створив теорію електромагнетизму (рівняння Максвелла), з яких випливало, що швидкість світла стала. Це стало викликом для класичної механіки Ньютона і згодом — стимулом до побудови релятивістської фізики. У 1861 Максвелл опублікував статтю "On Physical Lines of Force", де виклав ідеї про електромагнітне поле та ввів концепцію змінного електричного струму (тобто струму зміщення). У 1865 у праці "A Dynamical Theory of the Electromagnetic Field" він представив уже повний набір рівнянь, які описували взаємозв’язок електричних і магнітних полів. З цієї теорії випливало, що світло — це електромагнітна хвиля, яка поширюється у вакуумі з кінцевою швидкістю (що точно відповідала відомій швидкості світла).
У червні 1905 року (за кілька тижнів до статті Айнштайна!) Пуанкаре подав до Академії наук Франції статтю: "Про динаміку електрона" (Sur la dynamique de l’électron), де він: узагальнив перетворення Лоренца як групу; та сформулював принцип відносності як фундаментальний постулат.
Здавалося б Лоренц заклав основи математичного апарату релятивістської фізики. Пуанкаре його вдосконалив і сформулював принцип відносності. Що тут можна було б додати до завершення будови сучасної релятивістської фізики? Виявляється не все було так просто. Практично всі науковці тих часів вважали, що електромагнітні хвилі розповсюджуються в ефірі, який заповнює весь космічний простір. Проте численні експерименти по виявлення цього космічного середовища були безрезультатними. Тобто з математичним апаратом релятивістської фізики було все гаразд, а з філософським розумінням цієї нової фізики виникали проблеми. Потрібен був неординарний погляд на всю цю проблему. І такий погляд сформулював Айнштайн.
Він не запропонував жодної нової формули у будову релятивістської фізики, але запропонував взагалі відмовитись від ідеї ефіру, а перетворення Лоренца обгрунтовував не характером взаємодії реальних тіл, що рухались, з ефіром, а властивостями простору-часу. Релятивістська фізика була сформульована ним у вигляді послідовної концепції, грунтованої на двох постулатах: сталості швидкості світла і принципу відносності.
Анрі Пуанкаре (1854–1912) мав свій погляд на зв'язок між геометрією і властивостями простору. Ось декілька основних ідей, які він висловлював:
Релятивістська фізика створювалась зусиллями багатьох фізиків і математиків першої величини. Внесок кожного з них було настільки важко виділити, що за створення революційної фізичної теорії ніхто з науковців так і не отримав жодної нобелівської премії, а вона заслуговувала багатьох таких премій.
Тепер щодо ефіру. У часи створення релятивістської фізики люди і гадки не мали, що таке темна матерія і темна енергія. Слідом за Айнштайном всі вважали простір порожнім. Як можна говорити про якусь субстанцію типу ефіру у порожньому просторі? Астрономічні відкриття останніх десятиліть все змінили. У сучасній космології Всесвіт складається з:
-
Темної енергії — приблизно 68–70%
-
Темної матерії — приблизно 25–27%
-
Звичайної (баріонної) матерії — лише близько 5%
Ці цифри базуються на найновіших даних, зокрема з космічного мікрохвильового фону (CMB), які отримав супутник Planck. Коротко їх властивості:
-
Темна енергія (~70%) — прискорює розширення Всесвіту.
-
Темна матерія (~25%) — не випромінює світло, але має гравітаційний вплив (наприклад, утримує галактики разом).
-
Звичайна матерія (~5%) — усе, що ми можемо побачити (зірки, планети, люди тощо).
8.Чи заперечують досліди Майкельсона і Морлі існування ефіру?
Чи існує матеріальне середовище, у якому розповсюджуються електромагнітні хвилі? Від 19 сторіччя це середовище прийнято називати ефіром. Якщо ефір існує, то чи можна пов`язати з ним абсолютну систему відліку? Якщо такий ефір існує, то чи можна було б експериментально визначити рух небесних тіл відносно нього?
Мал. 1. Принципова схема установки Майкельсона і Морлі
З метою визначення можливого руху Землі відносно ефіру у 1887 році у Школі прикладних наук Кейса в м. Клівленді штату Огайо були здійснені знамениті досліди Альберта Майкельсона та Едварда Морлі. Перед дослідниками стояло завдання створення приладу, чутливого до руху Землі. В якості такого приладу був запропонований так званий інтерферометр Майкельсона.
Мал. 2. Сучасний вигляд установки Майкельсона і Морлі
В інтерферометрі початковий промінь розділяється на два за допомогою напівпрозорого дзеркала, а потім ці два промені, подолавши різний шлях, зводяться докупи й інтерферують. Характер інтерференційної картини свідчить про різницю шляхів, пройдені цими двома променями.
Мал. 3. Інтерференційна картина
Якщо Земля рухається відносно ефіру, то промінь, перпендикулярний до руху Землі, і промінь, паралельний до руху Землі, мали б по різному відчувати рух ефіру, а отже, долати різний оптичний шлях. Таким чином, під час обертання інтерферометра інтерференційний малюнок мав змінюватися. Проте спостережувані зміни інтерференційної картини знаходились в межах похибки експерименту і не дозволяли стверджувати, що рух Землі щодо ефіру вдалося зафіксувати.
Мал. 4. Траєкторія руху Землі у системі відліку, пов`язаної із Сонцем
Розглянемо спочатку очікуваний Майкельсоном і Морлі зсув інтерференційної картини. Для цього розглянемо інтерферометр з вдома взаємно перпендикулярними плечами однакової довжини L. Одне з цих плечей спрямуємо вздовж орбітального руху Землі, інше, відповідно, перпендикулярно йому. Нехай вздовж руху Землі буде спрямоване горизонтальне плече (Мал. 5)
Мал. 5. Схема досліду Майкельсона і Морлі
Поки світло рухається вздовж напрямку руху Землі і із швидкістю c відносно ефіру, відносно дзеркала, від якого воно має відбитись, воно рухається із швидкістю c-v. Тут v – швидкість, з якою рухається дзеркало відносно ефіру також рухаючись вздовж напрямку руху Землі. Час, за який світло досягне цього дзеркала буде t1 = L / (c - v). Відбившись від дзеркала світло почне рухатись у протилежному напрямку щодо руху Землі із швидкістю c+v відносно дзеркала. Зворотній шлях воно пройде за час t2 = L / (c + v). Отже, шлях туди і назад світло пройде за час
Tl = t1 + t2 = 2 L c / (c2 - v2).
Розглянемо тепер рух світла у напрямку, перпендикулярному руху Землі. Поки світло рухатиметься до дзеркала, розташованого на перпендикулярному плечі інтерферометра, час t3, це дзеркало, рухаючись вздовж напрямку руху Землі, пройде шлях v t3. Отже, світло із швидкістю c до моменту відбиття від цього дзеркала має пройти шлях, відповідно до теореми Піфагора, c t3 = √ (L2 + v2 t32). Такий же шлях світло пройде і після відбиття від дзеркала до початкової точки. Таким чином, шлях туди-назад світло пройде за час
Tt = 2 t3 = 2 L / √ (c2 - v2).
Різниця часів визначиться наступною формулою
ΔT = 2 L / c (1 / (1 - v2 / c2) – 1 / √(1 – v2 / c2)).
Обидва доданки в круглих дужках можна розкласти в ряд Маклорена за малим параметром v2 / c2, обмежившись першими двома членами. Тоді різниця часів дорівнюватиме
ΔT = (L / c) ( v2 / c2).
При повороті інтерферометра на дев`яносто градусів різниця часів мала б змінити знак із відповідним зміщенням інтерференційної картини. Величина цього ефекту була якраз такою, яку цілком можна було б спостерегти вже у 1887 році, не говорячи вже про наш час.
Мал. 6. Народження або анігіляція електрон-позитронних пар
Така невідповідність запропонованої теорії і реального експерименту вимагала вдосконалення теорії і таке вдосконалення було запропоноване Гендріком Антоном Лоренцом (1853-1928 рр.) у 1904 році. У фізику його відкриття ввійшло під назвою перетворень Лоренца. (Формули, що відомі зараз як перетворення Лоренца, першим вивів фізик Джозеф Лармор у 1900 році. Лоренц у 1904 році довів інваріантність системи рівнянь Максвелла відносно цих перетворень, проте фундаментальне положення сучасної фізики про рівноправність всіх інерційних систем відліку у нього було відсутнє. У 1905 році Анрі Пуанкаре узагальнив результати Лоренца та досяг повної коваріантності рівнянь електродинаміки. Саме Пуанкаре ввів у науковий обіг терміни перетворення Лоренца та група Лоренца.) Зокрема, з перетворень Лоренца випливало, що довжина тіла зменшується у напрямку його руху відповідно формулі
L = L0 √ (1 - v2 / c2).
Зауважимо, що довжина плеча інтерферометра, перпендикулярного руху Землі залишиться незмінною.
Таким чином, фундаментальне узагальнення фізики на предмет інваріантності всіх її рівнянь відносно перетворень Лоренца, тобто створення релятивістської фізики – фізики великих швидкостей, співмірних із швидкістю світла, дозволило пояснити негативний результат дослідів Майкельсона і Морлі. Але чи заперечують негативні результати цих дослідів існування ефіру, тобто матеріального середовища, в якому розповсюджуються всі взаємодії у природі? Альберт Айнштайн, який першим увів в обіг термін теорія відносності для позначення загально прийнятого тепер варіанту релятивістської фізики, вважав, що так - простір порожній. Це одна з основних засад запропонованого ним варіанта релятивістської фізики, відомого як теорія відносності. З ним не можна зв`язати жодної системи відліку, яку можна було б назвати виділеною серед інших або абсолютною. Рух – це завжди категорія відносна. Неможливо говорити про рух тіла, не пов`язуючи цей рух з іншим видимим тілом, яке відіграє роль системи відліку.
Мал. 7. Розподіл матерії у космічному просторі
Але чи досліди Майкельсона і Морлі однозначно свідчили на користь відсутності ефіру? Чи весь їх потенціал був використаний для спростування можливості визначити рух Землі відносно так званого ефіру? Легко показати, що ні. У класичних дослідах Майкельсона і Морді світ розповсюджувався у повітрі, показник заломлення якого n близький до одиниці. Тому швидкість світла у повітрі практично така ж, як і у вакуумі, тобто c. У разі прозорого середовища з показником заломлення суттєво більшим за одиницю ця швидкість була б c/n. Відповідно виписана вище формула для різниці часів проходження світлом різних плеч інтерферометру буде вже дещо іншою
ΔT = (2 n / c) (L / (1 - v2 n2/ c2) – L0 / √(1 – v2n2 / c2)).
Проте формула, що визначає скорочення довжини тіла, що рухається, буде тою самою, тобто показник заломлення в неї не входитиме. Цьому є просте пояснення: середовище, у якому розповсюджується світло, рухається разом з інтерферометром. Тепер різниця часів у квадратичному за часткою швидкостей наближенні буде наступною
ΔT = (n L0 / c) (n2- 1) (v2 / c2).
Сучасна точність вимірювань цілком здатна зафіксувати таке зміщення інтерференційної картини. Залишилось лише провести відповідні досліди.
Мал. 8. Роль темної енергії в еволюції всесвіту
Незалежно від можливих результатів таких дослідів, на сьогодні цілком впевнено можна стверджувати, що вакуум не є порожнім. Він є основним станом всіх відомих квантованих полів. Якщо матеріальними є поля, то матеріальним є і їх основний стан. З вакууму, за старою термінологією з ефіру, за певних умов народжуються пари, що складаються з частинок і античастинок різних видів. Видима матерія становить лише 4% реального світу навколо нас, що на сьогодні здатні зафіксувати наші прилади за допомогою електромагнітного поля. Існування решти матерії – 96% ми здатні фіксувати лише через її гравітаційне поле. Тобто вакуум – це, на сьогодні, найскладніша і цілком матеріальна субстанція, з якою має справу науковий світ. Простір не є порожнім. Можливо найближчим часом нам доведеться розпрощатись із ще одним міфом сучасної фізики.
Література
* А. А. Логунов. К работам Анри Пуанкаре О динамике єлектрона. Москва.-Институт ядерних исследований Академии наук СССР.- 1984.- С. 96.
В монографії міститься переклад двох класичних робіт Анрі Пуанкаре з релятивістської фізики з коментарями академіка А. А. Логунова:
1.А. Пуанкаре. О динамике єлектрона (5 июня 1905 года).
2.А. Пуанкаре. О динамике єлектрона (23 июня 1905 года).
З цих робіт видно, що релятивістська фізика у них сформульована у цілком сучасному вигляді.
Цим же роком датована і знаменита робота Альберта Айнштайна: Albert Eistein. Zur Elektrodynamik bewegter Körper. Annalen der Physik, (1905)
Рівняння Максвела
З
векторів напруженостей електричного і магнітного полів можна утворити бікватерніон
F = H + ic E.
У цього бікватерніона відсутня скалярна частина, а
векторна частина має комплексні коефіцієнти. Тобто це бікватерніон загального
типу без особливим властивостей симетрії. Переходу від однієї інерційної
системи відліку до іншої відповідає поворот цього бікватерніона у
бікватерніонному просторі без зміни модуля бікватерніона і цей оберт
здійснюється за загальний правилом з використанням вже знайденого вище
спеціального бікватерніона s, тобто
F` = s F S =
= (ic σ + s) F (ic σ - s) =
= F (1
– 2 s2) + 2 s (s F) – 2 ic σ [s × F]
або
(H + ic E)` = s (H + ic E) S =
= (H + ic E) (1 – 2 s2)
+ 2 s (s (H + ic E)) – 2 ic σ [s × (H + ic E)].
Звідси
H` = H (1 – 2 s2) + 2 s (s H) + 2 σ [s × E],
E` = E (1 – 2 s2)
+ 2 s (s E) – 2 σ [s × H].
Тут
(s H) = sx Hx + sy Hy + sz Hz,
(s E) = sx Ex + sy Ey + sz Ez,
[s × E] = │i, j, k; sx, sy, sz; Ex, Ey, Ez│ =
= i (sy Ez - sz
Ey) - j (sx Ez
- sz Ex) + k (sx
Ey – sy Ex),
[s × H] = │i, j, k; sx, sy, sz; Hx, Hy, Hz│ =
= i (sy Hz - sz
Hy) - j (sx Hz
- sz Hx) + k (sx
Hy – sy Hx).
Якщо оберт бікватерніона здійснюється у
площині x0t, останні формули матимуть вигляд,
тобто s = (sx, 0, 0), то
(s H) = sx Hx, (s
E) = sx Ex,
[s × E] = - j sx
Ez + k sx Ey,
[s × H] = - j sx Hz + k sx
Hy.
Тоді
Hx`
= Hx,
Hy`
= Hy (1 – 2 s2) - 2 σ sx Ez,
Hz`
= Hz (1 – 2 s2) + 2 σ sx Ey,
Ex` = Ex,
Ey` = Ey (1 – 2 s2)
- 2 σ sx Hz,
Ez`
= Ez (1 – 2 s2) + 2 σ sx Hy.
Якщо для компонент спеціального
бікватерніона скористатись вище знайденими виразами, то отримаємо наступний вислід
Ey` = [Ey + (V / c) Hz] / (1 – V2 / c2)1/2,
Ez` = [Ez – (V / c) Hy] / (1 – V2 / c2)1/2,
Hy` = [Hy + (V / c) Ez] / (1 – V2 / c2)1/2,
Hz` = [Hz – (V / c) Ey] / (1 – V2 / c2)1/2.
З цих формул
перетворення випливає дуже важливий висновок: розділення електромагнітного поля
на електричну і магнітну складову є досить умовним. Якщо в одній інерційній
системі відліку присутнє лише електричне поле, то в іншій інерційній системі
відліку є і електричне, і магнітне поле. Якщо в одній інерційній системі відліку
присутнє лише магнітне поле, то в іншій інерційній системі відліку є і магнітне,
і електричне поле.
Найважливішу
бікватерніонну функцію класичної електродинаміки можна утворити з векторного A(r, t) і скалярного φ(r, t) потенціалів
А = ic φ + A.
Тоді, скориставшись означенням бікватерніонного добутку,
nabla(A) = (ic ∂/с∂t + nabla) (ic φ + A) =
= - ∂φ/с∂t - div(A) + ic (∂A/с∂t + grad(φ)) – rot(A).
За означенням напруженостей електричного і магнітного
полів
E = - grad(φ) - ∂A/с∂t,
H = rot(A).
Оскільки спостережуваними величинами є напруженості
полів, то зручні для обчислень потенціали полів визначаються саме останніми
співвідношеннями. Видно, що потенціали з них визначені неоднозначно, а саме:
векторний потенціал визначений з точністю до градієнта довільної функції, а
скалярний – з точністю до похідної довільної функції
A` = A + grad(f),
φ` = φ - ∂φ/с∂t.
Штриховані і нештриховані потенціали призводять до
однакових напруженостей полів. Цю неоднозначність потенціалів можна використати
для спрощення бікватерніона nabla(A). Якщо потенціали полів обрати так, щоб
виконувалось співвідношення
∂φ/с∂t + div(A) = 0,
Яке називається калібровкою Лоренца, то бікватерніон nablaA матиме вигляд
nabla(A) = ic (∂A/с∂t + grad(φ)) – rot(A) = - H - ic E = - F.
Умовою бікватерніонної аналітичності будь-якої функції,
зокрема функції F, є рівність
нулю результату дії на неї спряженого бікватерніонного оператора набла.
nabla(F) = (ic ∂F/с∂t + div(F)) = (ic ∂(H + icE)/с∂t + rot(H + icE))= 0.
Виконавши
відповідне бікватерніонне множення, отримаємо
nabla(F) = {- ∂E/c∂t + rot(H)}+ ic {∂H/с∂t + rot(E)} + div(H) + ic div(E) = 0.
Звідси випливає, що і дійсна, і уявна частини скалярної і векторної частин бікватерніона
мають окремо дорівнювати нулю, тобто
- ∂E/c∂t + rot(H) = 0,
∂H/с∂t + rot(E) = 0,
div(H) = 0,
div(E) = 0.
У висліді ми отримали рівняння Максвела для
електричного і векторного полів у вакуумі у відсутності зовнішніх джерел заряду
і струму.
Якщо ввести у розгляд бікватерніон, що відопвідає густині заряда і електричному струму ic ρ + j, і порушити умову аналітичності за рахунок наявності джерел електричного і магнітного полів, то рівняння Максвела матимуть вигляд
- ∂E/∂t + rot(H) = j,
∂H/с∂t + rot(E) = 0,
div(H) = 0,
div(E) = ρ.
Широкому застосуванню бікватерніонів у класичній електродинаміці заважає відсутність детально розробленого математичного аналізу бікватерніонів. Якщо провадити аналогію з теоремою комплексного аналізу про лишки, то аналога такої теореми для бікватерніонів на даний момент не доведено.

















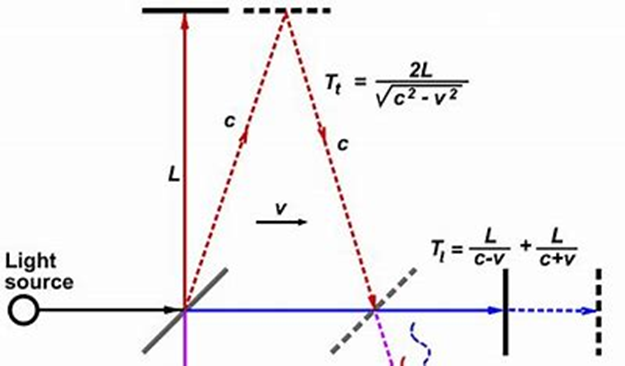
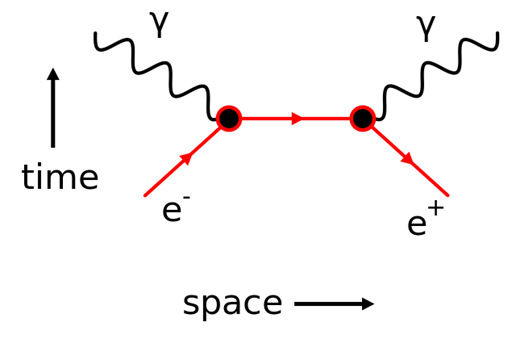






Немає коментарів:
Дописати коментар