Азартна гра. Нормальний розподіл

 

Йоган Ганс Фрідріх Гаус (1777 - 1855)

    Розглянемо азартну гру, тобто таку гру, де не існує виграшної стратегії. Виграш і програш  відбуваються довільним чином. Прикладами азартної гри є підкидання монети, грального кубика, рулетка і більшість картярських ігор. Формалізувати цю задачу можна у такий спосіб: На числовій осі розглянемо точку, що перебуває спершу у початку координат, а далі може абсолютно випадково рухатись стрибками на довільну відстань як у бік зростання значення її координати x, так і бік її зменшення. Додатні значення x відповідають виграшу відповідної суми, від`ємні – програшу. Нашою метою буде заходження функції розподілу ймовірностей координати цієї точки після великої кількості стрибків.

Виявляється, що цю задачу можна спростити, розглянувши блукання точки не на числовій прямій, а у площині. Тепер положення точки задаватиметься двома координатами x і y. Позначимо відповідну функцію розподілу ймовірності (густину розподілу ймовірності) через F(x, y). Тоді ймовірність точки мати координати x і y з діапазону значень [x, x+dx], [y, y+dy] позначиться так

                                    dW(x, y) = F(x, y) dx dy.

   Оскільки координати точки x і y абсолютно рівноправні і незалежні, то їх зміна відбувається за одним і тим же законом f(x) і f(y) і

                                          F(x, y) = f(x) f(y).

      Кожна з цих функцій задовольняє умові нормування

∫ f(x) dx = ∫ f(y) dy = 1.

 Оскільки рівноправними є також додатні і від`ємні значення кожної з координат, тобто

∫ F(x, y) dx dy = 1,   f(x) = f(-x),   f(y) = f(-y),   ∫ f(y) dy

 то відповідні густини ймовірностей залежать лише від квадратів цих координат

 f(x) = f(x²), f(y) = f(y²)

                Зовсім аналогічно рух точки можна описати і у полярних координатах ρ, φ

 dW(ρ, φ) = F(ρ, φ) ρ dρ dφ = R(ρ) Φ(φ) ρ dρ dφ.

 Кожна з густин у полярних координатах задовольняє умові нормування

 ∫ F(ρ, φ) ρ dρ dφ = 1,   ∫ R(ρ) ρ dρ = 1,   ∫ Φ(φ) dφ = 1.

 Густину розподілу за полярним кутом φ легко знайти з умови нормування, оскільки всі напрямки руху точки рівноправні ( цей кут визначає саме напрямок руху)

 Φ(φ) = 1 / 2 π.

 Тепер густину розподілу у полярних координатах можна записати так

 F(ρ, φ) = (1 / 2 π) R(ρ) = (1 / 2 π) R(x² + y²).

 Оскільки

dW(x, y) = dW(ρ, φ),   dx dy = ρ dρ dφ,

 то

f(x²) f(y²) = (1 / 2 π) R(x² + y²).

 Від функційного рівняння зручно перейти до диференційного. Для цього функційне рівняння спочатку логарифмуємо

ln[f(x²)] + ln[f(y²)] = - ln(2 π) + ln[R(x² + y²)].

 Тепер це рівняння спочатку здиференціюємо за x, а потім за y

 df(x²) / f(x²) = dR(x² + y²) / R(x² + y²),

 df(y²) / f(y²) = dR(x² + y²) / R(x² + y²),

 Оскільки ліві частини цих рівнянь рівні, то рівні і праві їх частини

 df(x²) / f(x²) = df(y²) / f(y²) = - λ.

 Тут λ – довільна стала. Її поява засвідчує той факт, що ми маєм рівність двох виразів, кожний з яких залежить від іншої змінної. Останнє рівняння еквівалентне системі двох рівнянь

df(x²) / f(x²) = - λ,   df(y²) / f(y²) = - λ.

     Загальні розв`язки цих рівняннь легко знаходяться і мають вигляд

         f(x²) = A exp(- λ x²),   f(y²) = A exp(- λ y²).

   

Довільні сталі можна знайти з умови нормування – це відомий інтеграл Пуассона

    

     A = λ^1/2 / π^1/2.

     Якщо позначити дисперсію цього розподілу через σ², то, за означенням,

    

     σ² = <x²> - <x>².

    

Обчислюючи дисперсію із знайденою нами функцією розподілу ймовірності отримаємо

         λ = 1 / 2 π σ².

    

      Остаточний вигляд знайденого нами розподілу ймовірності буде наступним

     f(x²) = [1 / σ (2 π)^1/2] exp(- x² / 2 σ²).

     

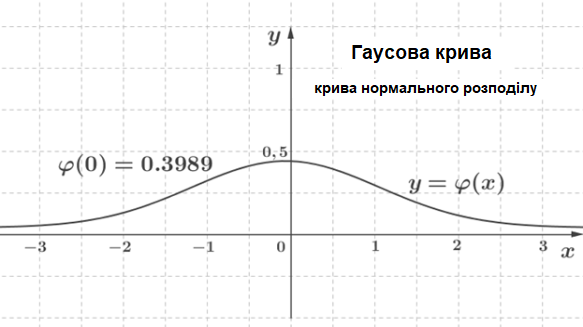
Такий розподіл називається нормальним розподілом або розподілом Гауса. Вище він записаний у разі нульового математичного сподівання μ. У загальному випадку

f(x²) = [1 / σ (2 π)^1/2] exp[- (x – μ)² / 2 σ²).

      

               Саме таким розподілом описується теплова взаємодія системи і термостату у стані термодинамічної рівноваги. Саме таким розподілом описується взаємодія пересічної людини і суспільства з точки зору матеріальних ресурсів. Людина щось бере від суспільства, десь працюючи, і якось витрачає зароблене. Ймовірність її різноманітних статків описується саме нормальним розподілом. Суспільство відповідальне за два параметри цього розподілу: математичне очікування μ, тобто середній рівень життя у даному суспільстві, і температуру T, тобто здатність пересічної людини заробляти більше від середнього рівня і також більше витрачати від середнього рівня витрат пересічної людини. Можливість заробляти більше завжди пов`язане з додатковим фізичним і розумовим навантаження і є певним випробуванням для здоров`я людини. У суспільстві мають існувати сприятливі умови для бажаючих заробляти більше. Можливість більше витрачати також завжди пов`язане з ризиком, але ризиком неповернення зайнятих десь грошей. Цей ризик мінімальний у стабільному, багатому, передбачуваному суспільстві і, фактично, виражає рівень оптимізму людини щодо свого майбутнього.

        Повертаючись до азартної гри зазначимо, що математичне очікування значення координати точки x – це очікування виграшу у разі її додатних значень і очікування програшу у разі її від`ємних значень. Нульове математичне сподівання у даному випадку означає, що чим довше людина грає в азартну гру, тим ближче значення її виграшу (вибіркове середнє) буде до математичного очікування, тобто до нуля. Отже, азартна гра з точки зору заробітку не має жодного сенсу. Насправді, виграш в окремому турі можливий, так само як і програш, проте за багато турів гравець приходить до математично строгого результату – нульового виграшу. Проте, враховуючи, що з кожного виграшу гравець сплачує певну його долю казино, а за кожного програшу казино нічого не сплачує гравцю, щоб хоча б частково компенсувати його втрати, маємо остаточний програш гравця у вислід багатьох турів. Тому, коли гравці, час від часу, виграють великі суми у якомусь з турів, працівники казино завжди пропонують їм пограти ще, нібито для того, щоб виграти ще більше. Проте, насправді, вони підштовхують гравця до тривалої гри, а математика гарантує нульовий виграш саме за тривалої гри.

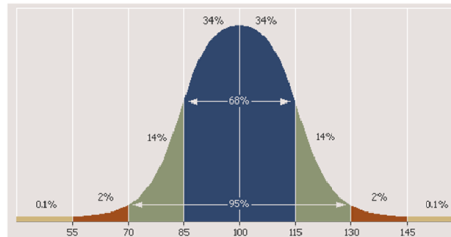
(Якщо сукупність всіх гравців взяти за 100%, то на графіку зазначені відсотки осіб з різними сумами програшів і виграшів. Загальна сума всіх програшів - 45 одиниць. Загальна сума всіх виграшів - 45 одиниць.)

               Чому ж люди грають в азартні ігри? Моя відповідь – через своє невігластво. Їм здається, що випадком можна керувати. Проте є і друга причина. Більшість людей за всяку ціну уникають розумового напруження. Чого не вимагає азартна гра, то це якраз розумового напруження. Нарешті, є і третя причина - найголовніша. Вона полягає у тому, що саме азартна гра урівнює шанси і на виграш, і на програш всіх гравців, не залежно від їх розумових здібностей і соціального статусу. Прагнення рівності – це найсильніший спонукальний мотив для дій людей, які інтуїтивно розуміють свою неконкурентноздатність порівняно з іншими людьми.

Національна асоціація дослідників Голодомору - геноциду українців | Публікація 26Національна асоціація дослідників Голодомору - геноциду українців | Публікація 15

Валерій Швець