Science with Shvets V. T.: Великий канонічний розподіл. Розподіли Больцмана, Фермі і Бозе

Великий канонічний розподіл ймовірності

Тепер ми розглянемо великий канонічний розподіл. Нехай дві макроскопічні системи, тобто такі, що складаються з великої кількості елементарних частинок, атомів, молекул або інших об`єктів знаходяться у стані рівноваги та механічному і тепловому контакті. Тобто вони обмінюються між собою не лише енергією, але і мікрочастинками. Одна з них маленька з енергією ϵ і кількістю частинок n, інша велика з енергією E-ε і кількістю частинок N-ε. Малість розуміється для енергій у сенсі ϵ<<E, для частинок n<<N. Більшу систему називатимемо термостатом. Саме вона визначає теплові і механічні характеристики малої системи. Останню називатимемо підсистемою. Далі, нехай термостат і підсистема разом утворюють замкнуту систему. Тобто ця система вже не обмінюється енергією і частинками з будь-якими іншими системами, а між собою підсистема і термостат обмінюються малими порціями енергії – малими порівняно з їх власними енергіями і малими кількостями частинок порівняно з їх власними кількостями. Це означає збереження загальної енергії замкнутої системи: E= E-ε+ϵ і загальної кількості частинок N-n+n. При цьому всі енергії також залежать від кількості частинок. Надалі це ми матимемо на увазі, для простоти, не позначаючи цей факт явно.

Термостат складається з великої кількості мікроскопічних частинок, окжна з яких має власну енергію. Сукупність цих енергій і кількості частинок і визначає макроскопічний енергетичний і механічний стани термостату. Проте, одну і ту ж сумарну енергію можна отримати колосальною кількістю стособів, кожний з який характеризує один з можливих варіантів розподілу цієї сумарної енергії між мікрочастинками. Кожний такий конкретний розподіл реалізує так званий мікроскопічний стан термостату. Отже, один макроскопічний стан термостату можна реалізувати величезною кількістю способів. Цю кількість називатимемо статистичною вагою стану або ступенем його виродження.

Якщо термостат і підсистема разом утворюють замкнуту систему з фіксованою енергією E, то мікростани системи реалізуються при енергії термостата E-ε і при енергії підсистеми ε. Термостат завжди складається з колосальної кількості мікрочастинок. У загальному випадку, підсистема також. Хоча часто розглядаються і підсистеми, що складаються лише з однієї мікрочастинки. Різноманітні комбінації мікростанів системи і термостату ще більше збільшують кількість мікростанів замкнутої системи, тобто статичну вагу її макростану.

З точки зору теорії ймовірностей кожний мікростан замкненої системи називається елементарною подією ω_i. Їх повна сукупність утворюють простір елементарних подій Ω. Сукупність елементарних подій, що реалізують стан підсистеми, утворюють подію Ω_ε,_n, яка відповідає стану підсистеми з енергією ε і кількістю частинок n. Сукупність елементарних подій, що реалізують стан термостата, утворюють подію Ω_E_-_ε_,_N_-_n, яка відповідає стану термостата з енергією E-ε.

Ймовірність елементарної події називається елементарною ймовірністю p(ω_i). Нехай P(Ω_ε,_n) – ймовірністю підсистеми мати енергію ε і кількість частинок n, P(Ω_E_-_ε_,_N_-_n) – ймовірність термостату мати енергію E-ε і кількість частинок N-n. Ці дві ймовірності надалі нас і цікавитимуть у першу чергу. Очевидно, що P(Ω)=1. Тепер у нас є формальна основа для подальших досліджень замкненої системи в рамках теорії ймовірностей, оскільки ми побудували ймовірнісний прості {Ω, A, P(A)}. Тут А – алгебра подій, тобто сукупність всіх подій разом з елементарними, замкнена відносно операцій додавання, віднімання, множення і заперечення, визначених для множин. Подальший алгоритм знаходження шуканих ймовірностей формально дуже простий. Для цього лише потрібно знайти суму елементарних ймовірностей, що формують ці ймовірності:

P(Ω_ε,_n) = p_ε_,_n_,1+ p_ε_,_n_,2 + … ,

P(Ω_E_-ε,_N_-_n) = p_E_-ε,_N_-_n_,1+ p_E_-ε,_N_-_n_,2 + … .

Але практично ця задача є нереальною через надзвичайно велику кількість елементарних подій, яким можуть відповідати різні елементарні ймовірності. Потрібні неминучі спрощення у підході до задачі. Таким спрощенням є припущення, що всі елементарні події рівноправні, тобто їх елементарні ймовірності однакові

p_ε_,_n₁= p_ε_,_n_,2 = … = p_E_-ε,_N_-_n_,1 = p_E_-ε,_N_-_n_,2 = … .

Якщо позначити через |Ω| - кількість елементарних подій, що утворюють простір елементарних подій, то для рівноправних елементарних подій

p = p_i= 1 / |Ω| .

Так само формально просто можна визначити і шукані ймовірності:

P(Ω_ε,_n) = p Γ(Ω_ε,_n),

P(Ω_E_-ε,_N_-_n) = p Γ(Ω_E_-ε,_N_-_n).

Тут Γ(Ω_ε,_n) і Γ(Ω_E_-ε,_N_-_n) - кількість елементарних подій, що утворюють події Ω_ε,_n, Ω_E_-ε,_N_-_n або статистичні ваги відповідних станів. Але навіть після такого радикального спрощення задача залишається нереально складною для розв`язання через надзвичайно велику кількість мікростанів, яку не можливо виміряти безпосередньо. Тому доцільно виразити статистичні ваги через якісь макроскопічні характеристики, наприклад, термостату або всієї замкнутої системи, які вже у той, чи інший спосіб можуть бути виміряні. Такою зручною характеристикою є ентропія. Вона визначається так

S(E) = ln[Γ(E)].

Ця макроскопічна характеристика також не вимірюється безпосередньо, але в рамках термодинаміки може визначатись іншими макроскопічними характеристиками системи, які вже вимірюються експериментально.

Якщо підсистема знаходиться у стані з енергією ε і кількістю частинок n із ймовірністю P(Ω_ε,_n), а термостат з енергією E-ε і кількістю частинок N-n із ймовірністю P(Ω_E_-ε,_N_-_n), то замкнута система буде знаходитись у стані з таким розподілом енергії і кількості частинок з ймовірністю, що визначається добутком попередніх ймовірностей

W(ε, n) = P(Ω_ε,_n, Ω_E_-ε,_N_-_n). = P(Ω_ε,_n) P(Ω_E_-ε,_N_-_n) = . p² Γ(Ω_ε,_n) Γ(Ω_E_-ε,_N_-_n).

Відповідно, можна говорити і про ймовірність знаходження нашої підсистеми, що є частиною замкнутої системи, з енергією ε і кількістю частинок n, у будь-якому мікроскопічному стані, поклавши Γ(Ω_ε)=1,

w(ε, n) = P(ω_ε,_n, Ω_E_-ε). = p(ω_ε) P(Ω_E_-ε,_N_-_n). =. p² Γ(Ω_E_-ε,_N_-_n) = p² exp[S(E-ε, N-n)].

Очевидно,

W(ε, n) = w(ε, n) Γ(Ω_ε,_n).

Наступного спрощення можна досягти, враховуючи малість енергії системи порівняно з енергією термостату ε<< E-ε і малість її кількості частинок n<<N-n. Розвинувши ентропію системи у ряд Маклорена за степенями ε і n, матимемо

S(E-ε, N-n) = S(E, N) – [ꝺS(E, N)/ꝺE]_N ε – [ꝺS(E, N)/ꝺN]_E n + O(ε²) + O(n²).

Але за означенням абсолютної температури T

T^-1 = [ꝺS(E, N)/ꝺE]_N.

T – абсолютна температура замкнутої системи. Ця температура легко вимірюється експериментально. Одночасно, це є температура і термостату, і підсистеми, якщо остання є макроскопічною і складається з великої кількості мікрочастинок, оскільки вони знаходяться у стані теплової рівноваги між собою. Якщо ж підсистемою вважається лише одна мікрочастинка, то тоді мова йде лише про температуру термостата.

За означенням хімічного потенціалу

μ / T = - [ꝺS(E,N)/ꝺN]_E.

Хімічний потенціал також є характеристикою всієї замкненої системи, оскільки підсистема і термостат знаходяться у стані механічної рівноваги між собою. Якщо підсистема складається лише з однієї мікрочастинки, то хімічний потенціал є характеристико лише термостата. Для систем із змінною кількістю частинок у стані механічної рівноваги хімічний потенціал відіграє роль, подібну температурі у разі теплової рівноваги. Тепер вираз для шуканої ймовірності можна записати у вигляді

W(ε,n) = P(Ω_ε,_n, Ω_E_-ε,_N_-_n). = P(Ω_ε,_n) P(Ω_E_-ε,_N_-_n). =. p² Γ(Ω_ε,_n) Γ(Ω_E_-ε,_N_-_n) =

= p² Γ(Ω_ε,_n) exp[ S(E,N) + (μ n -ε) / T].

Після зроблених наближень ймовірність того, що замкнута система знаходиться у стані, що визначається мікроскопічними станами термостата і підсистеми, перестала залежати від мікроскопічних станів термостату. Тепер вона залежить лише від мікроскопічних станів підсистеми. Залежність від мікроскопічних станів термостату трансформувалась у залежність ймовірності від такої експериментально вимірюваної характеристики термостату як абсолютна температура, такої макроскопічної термодинамічної характеристики термостату і всієї замкнутої системи як хімічний потенціал та залежність від ентропії замкнутої системи. Дану ймовірність можна перетворити у ймовірність, що характеризує виключно підсистему, точніше ймовірність її знаходження у мікроскопічних станах з різними енергіями ε і кількостями частинок n. Для цього її необхідно лише відповідним чином нормувати

∑ W(ε, n) = p² exp[S(E)] ∑ Γ(Ω_ε,_n) exp[(μ n -ε ) / T] = 1.

Умова нормування дозволяє визначити сталі величини p² exp[S(E,N)], які визначаються лише властивостями всієї замкнутої системи, через мікроскопічні характеристики підсистеми. Суму за всіма мікростанами називають великою статистичною сумою

Z(μ, T) = ∑ Γ(Ω_ε,_n) exp[(μ n - ε) / T].

Остаточний результат для ймовірностей різних енергетичних станів підсистеми, що знаходиться у довільному мікростані, буде таким

W(ε, n) = Z^-1(μ, T) exp[(μ n - ε) / T] Γ(Ω_ε).

Якщо ж мова йде про ймовірність знаходження підсистеми з даним значенням енергії у конкретному мікростані, то відповідна ймовірність буде наступною

w(ε, n) = Z^-1(μ, T) exp[(μ n - ε) / T].

Тепер термостат впливає на ймовірності мікростанів підсистеми лише через такі свої макроскопічні характеристики як абсолютна температура і хімічний потенціал.

Отриманий закон розподілу називається великим канонічним або розподілом Гіббса. Всі складності його використання пов`язані із знаходженням статистичної суми. У кожній конкретній задачі мусять бути свої спрощуючі обставини, що дозволяють це зробити. Дві характеристики мають бути відомими, часто це вдається зробити на основі мікроскопічних розрахунків, - це енергетичний спектр підсистеми і статистична вага кожного її енергетичного стану.

У виразі для великого канонічного розподілу ймовірності велику статистичну суму можна замінити макроскопічною термодинамічною характеристикою підсистеми. Цією характеристикою називається термодинамічний потенціал Ω. За означенням

Ω = - T ln[Z(μ, T)].

У загальному випадку, для системи обсягом V,

Ω = Ω(μ, T, V).

Термодинамічний потенціал підсистеми пов`язаний з її вільною енергією і хімічним потенціалом наступним чином

Ω = F – μ n.

Тепер закон розподілу ймовірностей матиме вигляд

w(ε ,n) = exp[(Ω + μ n - ε) / T].

Якщо закон розподілу енергетичних станів підсистеми відомий, то середнє значення будь-якої функції, що визначається тим самим енергетичним спектром, можна знайти у стандартний для математичної статистики спосіб

< f(ε,n)> = ∑∑ f(ε,n) W(ε,n).

І у разі великого канонічного розподілу ентропію системи можна виразити через функцію розподілу ймовірності

S = - ∑ W(ε, n) ln[w(ε, n)] = - ∑ w(ε, n) ln[w(ε, n)] Γ(Ω_ε,n).

Формули для статистичної суми математичного очікування (середнього значення фізичної величини) записані для найпростішого випадку – дискретного енергетичного спектру. Саме тому скрізь у нас присутні суми. У разі неперервного спектру замість сум мають бути інтеграли. Перехід від дискретного спектру до неперервного вимагає окремого детального розгляду і ми це зробимо на прикладах конкретних задач.

Розподіл Больцмана

Великий канонічний розподіл дозволяє знайти середню кількість мікрочастинок, що утворюють підсистему. За означенням

M n = <n> = - ꝺΩ(μ, T, V) / ꝺμ =

= T ꝺln[Z(μ, T, V)] / ꝺμ = T [Z(μ, T, V)]^-1 ꝺZ(μ, T, V) / ꝺμ =

= T [Z(μ, T, V)]^-1ꝺ ∑_m ∑_εΓ(Ω_ε,_m) exp[(μ m – ε(m)) / T] / ꝺμ =

= [Z(μ, T, V)]^-1∑_m m ∑_εΓ(Ω_ε,_m) exp[(μ m – ε(m)) / T]..

Ми знайшли середню кількість мікрочастинок підсистеми, яка може обмінюватись з термостатом не лише енергією, але і частинками. В якості підсистем можна розглядати частинки даної підсистеми, що знаходяться у її різних енергетичних станах ε. Загальну кількість частинок підсистеми можна представити так

n = ∑_ε <n_ε>,

де середня кількість частинок підсистеми у стані ε визначається так

<n_ε> = [Z_ε(μ, T, V)]^-1∑_m m exp[(μ m – ε(m)) / T].

Статистична сума для підсистеми, що складається з частинок у стані з енергією ε, дорівнює

Z_ε(μ, T, V) = ∑_m exp[(μ m – ε(m)) / T].

Цю статистичну суму можна обчислити за ряду спрощуючих обставин. Такими обставинами можуть бути відсутність взаємодії між частинками та високі температури, коли ε(m)=εm і (μm-ε)/T<<1. Тоді кількість станів значно перевищуватиме кількість частинок, тобто <n_ε><<1. У цьому разі статистична сума просто дорівнює 1. У сумі за кількістю частинок суттєвим буде лише перший, відмінний від нуля доданок з m=1. Отже,

<n_ε> = exp[(μ - ε) / T].

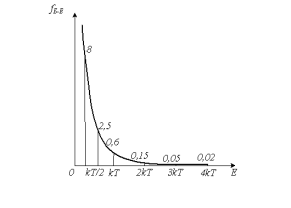
Такий розподіл для кількості частинок у стані з енергією ε називається розподілом Больцмана. Його можна записати і у іншому вигляді, враховуючи, що

Людвіг Едуард Больцман (1844 - 1906)

∑_ε <n_ε> = ∑_ε exp[(μ - ε) / T] = exp(μ / T) ∑_ε exp(- ε / T) = T exp(μ / T) = n.

Таким чином,

<n_ε> = (n / T) exp(- ε / T).

Це є ніщо інше як показниковий розподіл ймовірності.

Розподіл Фермі

Спрощення вихідної формули відбувається і у разі, якщо температура є низькою, тобто (μm-ε)/T>>1. Взаємодією між частинками будемо нехтувати, як і раніше. Для низьких температур важливими є квантові властивості підсистеми. Це виявляється у тому, що хвильова функція, що описує поведінку навіть системи невзаємодіючих частинок має бути або симетричною, відносно перестановки частинок, або антисиметричною. Така взаємодія називається обмінною У першому випадку ми маємо справу з Бозе-частинками, у другому випадку – з Фермі-частинками. Приналежність частинки до того, чи іншого класу визначається її власним моментом кількості руху – спіном. Якщо він цілий, то ми маємо справу з Бозе частинками, якщо напівцілий, - Фермі-частинками. З іншого погляду Бозе-частинки є переносниками взаємодії між Фермі-частинками. Типовими ферміонами є протони і електрони. Типовими бозонами є фотони. Специфіка Фермі-частинок полягає у тому, що у кожному квантовому стані може знаходитись не більше однієї частинки. У цьому разі статистична сума легко обчислюється, оскільки достатньо взяти лише перші два доданки суми за кількістю частинок,

Розподіл Фермі для різних температур

Z_ε(μ, T, V) = ∑_n exp[(μ n – ε(n)) / T] = ∑_n exp[(μ n – ε n) / T].=

. = 1 + exp[(μ – ε) / T].

Тепер для функції розподілу середньої кількості частинок за станами матимемо

Розподіл фотонів (Бозе-частинок) за енергією

<n_ε> = [1 + exp[(μ – ε) / T]]^-1exp[(μ – ε) / T]

або

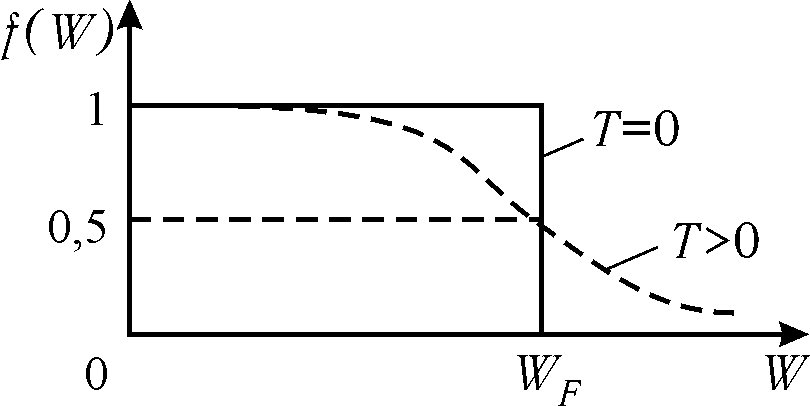
<n_ε> = 1 / [exp[(ε - μ) / T] + 1],

Цей розподіл називається розподілом Фермі.

Енріко Фермі (1901 - 1954)

Розподіл Бозе

Для Бозе-частинок жодних обмежень на їх кількість у довільному стані немає. У цьому разі

Z_ε(μ, T, V) = ∑_m exp[(μ m – ε(n)) / T] = ∑_m exp[(μ m – ε m) / T] =

= ∑_m {exp[(μ – ε) / T]}^m .

Тут ми маємо нескінчену геометричну прогресію. Вона збігається лише у разі, якщо її знаменник менше за одиницю, тобто exp[(μ–ε)/T]<1. У цьому разі

Z_ε(μ, T, V) = 1 / [1 - exp[(μ – ε) / T]].

Для середньої кількості частинок у стані з енергією ε отримаємо

<n_ε> = exp[(μ – ε) / T] / [1 - exp[(μ – ε) / T]] = 1 / [exp[(ε - μ) / T - 1].

Розподіл Бозе також нормований на загальну кількість частинок і не є ймовірність. Перетворити його у розподіл ймовірності можна поділивши обидві частини останньої рівності на загальну кількість частинок. Недолік такого запису такий же як і у разі розподілу Фермі, тому він і не набув популярності.

У випадку великих температур exp[(μ–ε)/T]<<1 і розподіл Фермі, і розподіл Бозе переходять у розподіл Больцмана.