Формула свободи. Канонічний розподіл ймовірності

 

                                             Гібс, Джозайя Уілард (1839 - 1903)

Зміст

Канонічний розподіл ймовірності

Канонічний розподіл і ентропія. Формула свободи. Ентропія і інформація

 Канонічний розподіл ймовірності

                  Мікроканонічний, канонічний і великий канонічний розподіли відіграють засадничу роль у статистичній фізиці. Тут ми розглянемо канонічний розподіл. Нехай дві макроскопічні системи, тобто такі, що складаються з великої кількості елементарних частинок, атомів, молекул або інших об`єктів знаходяться у стані рівноваги і тепловому контакті. Одна з них маленька з енергією ϵ, інша велика з енергією E-ε. Малість розуміється у сенсі енергії ϵ<<E. Більшу систему називатимемо термостатом. Саме вона визначає теплові характеристики малої системи. Останню називатимемо підсистемою. Далі, нехай термостат і система разом утворюють замкнену систему. Тобто ця система вже не обмінюється енергією з будь-якими іншими системами, а між собою підсистема і термостат обмінюються малими порціями енергії – малими порівняно з їх власними енергіями. Це означає збереження загальної енергії замкнутої системи: E = E-ε+ϵ. Статистичний закон, що описує цей обмін буде розглянутий окремо. Зараз для нас важливий сам факт такого обміну, який, власне, призводить систему у стан теплової рівновани з термостатом. 

              Термостат складається з великої кількості мікроскопічних частинок, окжна з яких має власну енергію. Сукупність цих енергій і визначає макроскопічний енергетичний стан термостату. Проте, одну і ту ж сумарну енергію можна отримати колосальною кількістю стособів, кожний з який характеризує один з можливих варіантів розподілу цієї сумарної енергії між мікрочастинками.  Кожний такий конкретний розподіл реалізує так званий мікроскопічний стан термостату. Отже, один макроскопічний стан термостату можна реалізувати величезною кількістю способів. Цю кількість називатимемо статистичною вагою стану або ступенем його виродження.

      Розглянемо простий приклад. Нехай наша система складається з двох мікрочастинок з енергіями ε₁ і ε₂. Відповідно, енергія системи ε=ε₁+ε₂. Якщо енергія системи ε=0, то цьому стану системи відповідає лише один мікростан: ε₁=0, ε₂=0. Якщо енергія системи ε=Δ, де Δ – нероздільна порція енергії, то тут ми маємо вже два мікростани: ε₁=Δ, ε₂=0 або ε₁=0, ε₂=Δ. Якщо енергія системи ε=2Δ, то тут ми маємо вже три мікростани: ε₁=2Δ, ε₂=0, або ε₁=0, ε₂=2Δ, або ε₁=Δ, ε₂=Δ. Статистична вага кожного наступного енергетичного стану системи наростатиме із збільшенням енергії системи, як також і із збільшенням кількості мікрочастинок в ній.

               Якщо термостат і підсистема разом утворюють замкнуту систему з фіксованою енергією E, то мікростани системи реалізуються при енергії термостата E-ε і при енергії підсистеми ε. Термостат завжди складається з колосальної кількості мікрочастинок. У загальному випадку, підсистема також. Хоча часто розглядаються і підсистеми, що складаються з однієї мікрочастинки. Різноманітні комбінації мікростанів системи і термостату ще більше збільшують  кількість мікростанів замкненої системи, тобто статичну вагу її макростану.

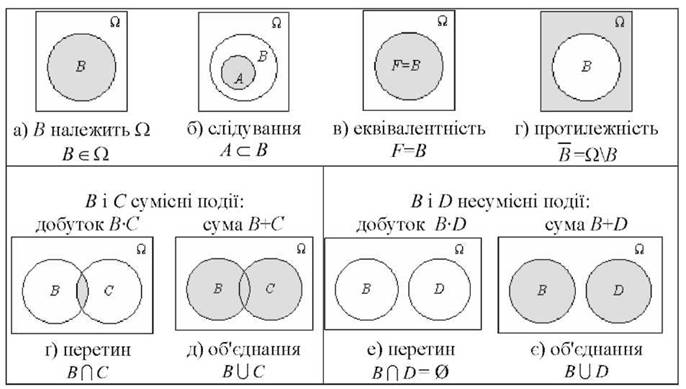
               З точки зору теорії ймовірностей кожний мікростан замкненої системи називається елементарною подією ω_i. Їх повна сукупність утворюють простір елементарних подій Ω. Сукупність елементарних подій, що реалізують стан підсистеми, утворюють подію Ω_ε, яка відповідає стану підсистеми з енергією ε. Сукупність елементарних подій, що реалізують стан термостата, утворюють подію Ω_E-ε, яка відповідає стану термостата з енергією E-ε. 

Простір елементарних подій, дії над подіями

Ймовірність елементарної події називається елементарною ймовірністю p(ω_i). Нехай P(Ω_ε) – ймовірністю підсистеми мати енергію ε, P(Ω_E-ε) – ймовірність термостату мати енергію E-ε. Ці дві ймовірності надалі нас і цікавитимуть у першу чергу. Очевидно, що P(Ω)=1. Тепер у нас є формальна основа для подальших досліджень замкненої системи в рамках теорії ймовірностей, оскільки ми побудували ймовірнісний прості {Ω, A, P(A)}. Тут А – алгебра подій, тобто сукупність всіх подій разом з елементарними, замкнена відносно операцій додавання, віднімання, множення і заперечення, визначених для множин. Подальший алгоритм знаходження шуканих ймовірностей формально дуже простий. Для цього лише потрібно знайти суму елементарних ймовірностей, що формують ці ймовірності:

                                          P(Ω_ε) = p_ε1+ p_ε2 + … ,

 P(Ω_E-ε) = p_{E-ε 1}+ p_{E-ε 2} + … .

Але практично ця задача є нереальною через надзвичайно велику кількість        елементарних подій, яким можуть відповідати різні елементарні ймовірності. Потрібні неминучі спрощення у підході до задачі. Таким спрощенням є припущення, що всі елементарні події рівноправні, тобто їх елементарні ймовірності однакові

                                           p_ε1 = p_ε2 = … = p_{E-ε 1} = p_{E-ε 2} = … .

Така гіпотеза називається ергодичною. Вона і досі не перетворилась у теорему із строгим доведенням.

 Якщо позначити через |Ω| - кількість елементарних подій, що утворюють простір елементарних подій, то для рівноправних елементарних подій

                                               p = p_i= 1 / |Ω| .

 

Так само формально просто можна визначити і шукані ймовірності:

                                                         

                                                            P(Ω_ε) = p Γ(Ω_ε),

        P(Ω_E-ε) = p Γ(Ω_E-ε).

 Тут Γ(Ω_ε) і Γ(Ω_E-ε) кількість елементарних подій, що утворюють події Ω_ε, Ω_E-ε або статистичні ваги відповідних станів. Але навіть після такого радикального спрощення задача залишається нереально складною для розв`язання через надзвичайно велику кількість мікростанів, яку не можливо виміряти безпосередньо. Тому доцільно виразити статистичні ваги через якісь макроскопічні характеристики, наприклад, термостату або всієї замкнутої системи, які вже у той, чи інший спосіб можуть бути виміряні. Такою зручною характеристикою є ентропія. Вона визначається так

 

S(E) = ln[Γ(t)].

 

Ця макроскопічна характеристика також не вимірюється безпосередньо, але в рамках термодинаміки може визначатись іншими макроскопічними характеристиками системи, які вже вимірюються експериментально.

               Якщо підсистема знаходиться у стані з енергією ε із ймовірністю P(Ω_ε), а термостат з енергією E-ε із ймовірністю P(Ω_E-ε), то замкнута система буде знаходитись у стані з таким розподілом енергії з ймовірністю, що визначається добутком попередніх ймовірностей

 

W(ε) = P(Ω_ε, Ω_E-ε). = P(Ω_ε) P(Ω_E-ε) = . p² Γ(Ω_ε) Γ(Ω_E-ε).

 

Відповідно, можна говорити і про ймовірність знаходження нашої підсистеми, що є частиною замкнутої системи, з енергією ε, у будь-якому мікроскопічному стані, поклавши Γ(Ω_ε)=1,

 w(ε) = P(ω_ε, Ω_E-ε). = p(ω_ε) P(Ω_E-ε). =. p² Γ(Ω_E-ε) = p² exp[S(E-ε)].

 

Очевидно,

W(ε) = w(ε) Γ(Ω_ε).

 

               Наступного спрощення можна досягти, враховуючи малість енергії системи порівняно з енергією термостату ε<< E-ε. Розвинувши ентропію системи у ряд Маклорена за степенями ε, матимемо

 

S(E-ε) = S(E) - dS(E)/dE ε + O(ε²).

 

Але за означенням абсолютної температури T

 

T^-1 = dS(E)/dE.

 

T – абсолютна температура замкнутої системи. Ця температура легко вимірюється експериментально. Одночасно, це є температура і термостату, і підсистеми, якщо остання є макроскопічною і складається з великої кількості мікрочастинок, оскільки вони знаходяться у стані теплової рівноваги між собою. Якщо ж підсистемою вважається лише одна мікрочастинка, то тоді мова йде лише про температуру термостата. У загальному випадку

 

S = S(E, T).

Тепер вираз для шуканої ймовірності можна записати у вигляді

 

W(ε) = P(Ω_ε, Ω_E-ε) = P(Ω_ε) P(Ω_E-ε) = p² Γ(Ω_ε) Γ(Ω_E-ε) = p² Γ(Ω_ε) exp[ S(E)-ε / T ].

 

Після зроблених наближень ймовірність того, що замкнута система знаходиться у стані, що визначається мікроскопічними станами термостата і підсистеми, перестала залежати від мікроскопічних станів термостату. Тепер вона залежить лише від мікроскопічних станів підсистеми. Залежність від мікроскопічних станів термостату трансформувалась у залежність ймовірності від такої експериментально вимірюваної характеристики термостату як абсолютна температура і залежність ентропії замкнутої системи від її енергії. Дану ймовірність можна перетворити у ймовірність, що характеризує виключно підсистему, точніше ймовірність її знаходження у мікроскопічних станах з різними енергіями ε. Для цього її необхідно лише відповідним чином нормувати

 

∑ W(ε) = p² exp[ S(E) ] ∑ Γ(Ω_ε) exp(-ε / T ) = 1.

 

Умова нормування дозволяє визначити комбінацію сталих величин p² exp[S(E)], які визначаються лише властивостями всієї замкненої системи, через мікроскопічні характеристики підсистеми. Суму за всіма мікростанами називають статистичною сумою

 

Z = ∑ Γ(Ω_ε) exp(-ε / T ).

 

Остаточний результат для ймовірностей різних енергетичних станів підсистеми, що знаходиться у довільному мікростані, буде таким

 

Канонічний розподіл Гібса

 

w(ε) = Z^-1 exp(-ε / T ).

 

Якщо ж мова йде про ймовірність знаходження підсистеми з даним значенням енергії у конкретному мікростані, то відповідна буде наступною

 

w(ε) = Z^-1 exp(-ε / T ).

 

Тепер термостат впливає на ймовірності мікростанів підсистеми лише через таку свою макроскопічну характеристику як абсолютна температура.

               Отриманий закон розподілу називається канонічним або розподілом Гібса. Всі складності його використання пов`язані із знаходженням статистичної суми. У кожній конкретній задачі мусять бути свої спрощуючі обставини, що дозволяють це зробити. Дві характеристики мають бути отримані, часто це вдається зробити на основі мікроскопічних розрахунків, - це енергетичний спектр підсистеми і статистична вага кожного її енергетичного стану.

         Якщо закон розподілу енергетичних станів підсистеми відомий, то середнє значення будь-якої функції, що визначається тим самим енергетичним спектром, можна знайти у стандартний для математичної статистики спосіб

 

< f(ε)> = ∑ f(ε) W(ε).

 

   Формули для статистичної суми математичного очікування (середнього значення фізичної величини) записані для найпростішого випадку – дискретного енергетичного спектру. Саме тому скрізь у нас фігурують суми. У разі неперервного спектру замість сум мають бути інтеграли. Перехід від дискретного спектру до неперервного вимагає окремого детального розгляду і це зробимо на прикладі конкретних задач.

Енергетичний спектр атома водню (по вертикалі - енергія)

      Традиційно розподіл Гіббса використовують для статистичного опису фізичних систем, що складаються з елементарних частинок, атомів, молекул. Проте так само успішно його можна застосувати і при розгляді будь-яких систем, що складаються з подібних елементів довільної структури, наприклад, це можуть бути людські спільноти. Що складаються з окремих людей. Останнє застосування не є традиційним, тому ми детально його обговорюватимемо для ряду конкретних випадків нижче.

Неперервний енергетичний спектр (по горизонталі - енергія)

            Приклад. Обчислимо статистичну, математичне сподівання і дисперсію для випадкової величини ε, розподіленої за канонічним законом для квазінеперервного енергетичного спектру, енергетичні рівні якого розташовані еквідистантно.

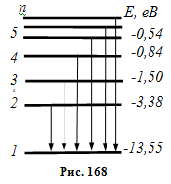
   Розв`язання. Еквідистантність енергетичних рівнів означає, що

 

ε_n = Δε n,   n = 0, 1, 2, … .

 

Квазінеперервність означає, що Δε << T і може використовуватись в якості зручної одиниці вимірювання температури. У цьому разі для статистичної суми маємо нескінчену геометричну прогресію із знаменником набагато меншим від одиниці

 

Z = ∑ exp( - ε_n / T*) = ∑ exp( - Δε n / T*) = ∑ exp( - Δε / T*)ⁿ =

 

= 1 / [1 - exp( - Δε / T*)] = T* / Δε = T.

 

Тепер канонічний розподіл набере вигляду

     

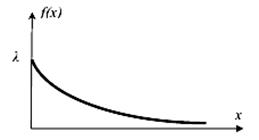
      w(ε) = T^-1 exp(-ε / T).

Тут λ=1/T

     

У математичній статистиці такий розподіл називається показниковим. Легко показати, що

      М ε = (1 / T) ∑ ε_n exp( - ε_n / T) = - (1 / T) (d / d(1/T)) ∑ exp( - ε_n / T) =

 

= - (1 / T) (d / d(1/T)) T = T,

 

М ε² = (1 / T) ∑ ε_n² exp( - ε_n / T) = (1 / T) (d² / d(1/T)²) ∑ exp( - ε_n / T) =

 

= (1 / T) (d² / d(1/T)²) T = 2 T².

 

D ε² = М ε² – (М ε)² = T².

 
 

Канонічний розподіл і ентропія. Формула свободи. Ентропія і інформація

Канонічний розподіл ймовірності можна виразити через вільну енергію підсистеми. Вільна енергія наступним чином пов`язана із статистичною сумою підсистеми

F = - ln( Z ).

       Вільна енергія є макроскопічною характеристикою речовини – термодинамічним потенціалом, що залежить від температури і об`єму підсистеми і вже може вимірюватись експериментально. У загальному випадку для системи з об`ємом V

F = F(T, V).

 Вільна енергія пов`язана з внутрішньою енергією E і ентропією S підсистеми наступним чином

 F = E – T S.

Канонічний розподіл тепер можна записати так

 w(ε) = exp[( F-ε ) / T ].

            Обчислимо тепер наступний середнє значення логарифму ймовірності знаходження підсистеми у її довільному мікроскопічному стані

 ∑ W(ε) ln[ w(ε) ] = ∑ W(ε) ( F-ε) / T = ( F- E ) / T.

 Тут внутрішня енергія, за означенням, є середнім значення енергії підсистеми

 E = ∑ W(ε) ε.

 Тепер шуканий вираз стане таким

 S = - ∑ W(ε) ln[ w(ε) ] = - ∑ w(ε) ln[ w(ε) ] Γ(Ω_ε).

Тобто функція розподілу ймовірностей дозволяє безпосередньо обчислювати ентропію, не залучаючи до обчислень жодних інших величин. Цей вираз широко використовується не лише у статистичній фізиці, але і у теорії інформації та інших застосування, пов`язаних з канонічним розподілом. 

         Припустимо, що всі енергетичні стани підсистеми невироджені, їх загальна кількість скінчена і дорівнює N, а ймовірності всіх станів однакові і дорівнюють w(ε)=1/N. У цьому разі вираз для ентропії максимально спрощується і

 S = ln(N).

 У теорії інформації ця формула називається формулою Хартлі.

 

Клод Шенон - творець теорії інформації

                        Приклад 1. Розглянемо приклад з теорії інформації. З території Московії у бік України стартувала балістична ракета з великим боєзарядом по одному з 8 найбільших міст України. По якому саме місту точно не відомо. Знайти кількість інформації, що міститься у цьому повідомленні.

                        Розв`язання. У даному разі простір елементарних подій складається з восьми елементарних подій. Всі вони рівноправні. З умови нормування ймовірності випливає, що ймовірність кожної елементарної події є 1/8. Кількість інформації I в повідомленні визначається за тою ж формулою, що і ентропія. Теорії інформації прийнято використовувати не натуральний логарифм, а логарифм за основою 2. Отже, кількість інформації дорівнює

I = log₂(8) = 3.

                Приклад 2. Розглянемо ще один приклад з теорії інформації. З території Московії стартувала балістична ракета з великим у боєзарядом у напрямку Одеси. Знайти кількість інформації, що міститься у цьому повідомленні.

                       Розв`язання. У даному разі простір елементарних подій складається з однієї елементарної події. Отже, кількість інформації дорівнює

 I = log₂(1) = 0.

Ми бачимо, що інформаційне повідомлення тим цінніше, чим більшу невизначеність воно у себе містить. З практичних міркувань очевидно, що перше з наведених повідомлень вимагає вжиття більшої кількості заходів через велику невизначеність інформації. У другому повідомленні мова йде про достовірну (вірогідну) подію, тобто воно не містить жодної невизначеності і вимагає для прийняття правильного рішення менше практичних зусиль.

             Приклад 3. Розглянемо приклад з соціології. Припустимо, що у Китаї проводяться президентські вибори. На цю посаду висунуто одного кандидата від однієї партії. Яка свобода політичного вибору реалізується в цій країні?

      Розв`язання. Для кількісного аналізу рівня політичної свободи можна використовувати ту саму формулу, що і у статистичній фізиці та теорії інформації Тут простір елементарних подій складається з однієї елементарної події, то для величини політичної свободи отримуємо

Svoboda = S = log₂(1) = 0.

         Приклад 4. Розглянемо ще один приклад з соціології. Припустимо, що у Сполучених штатах проводяться президентські вибори. На цю посаду висунуто одного кандидата від республіканської партії і одного кандидата від демократичної партії. Яка свобода політичного вибору реалізується в цій країні?

                  Розв`язання. Тут простір елементарних подій складається з двух елементарних подій. Традиційно за обох кандидатів голосує приблизно той самий відсоток виборців з невеликою перевагою на користь одного з кандидатів. Для простоти вважатимемо зазначені події рівноправними, тобто відповідні елементарні ймовірності дорівнюватимуть по 1/2.

Svoboda = S = log₂(2) = 1.

                 Приклад 5. Розглянемо ще один приклад з соціології. Припустимо, що в Україні проводяться президентські вибори. На цю посаду висунуто одного кандидата від республіканської партії і одного кандидата від демократичної партії. Яка свобода політичного вибору реалізується в цій країні, за відомими результатами цих виборів?

Кандидат	Кількість голосів	%	Висунення
Кравчук Леонід Макарович	19 643 481	59	Самовисування
Чорновіл В'ячеслав Максимович	7 420 727	23,27	Народний рух України
Лук'яненко Левко Григорович	1 432 556	4,49	Українська республіканська партія
Гриньов Володимир Борисович	1 329 758	4,17	Партія демократичного відродження України
Юхновський Ігор Рафаїлович	554 719	1,74	Самовисування
Табурянський Леопольд Іванович	182 713	0,57	Народна партія
Проти всіх/недійсні	1 327 788	4,07

             Розв`язання. Тут простір елементарних подій складається з семи елементарних подій відповідно до кількості кандидатів. В якості елементарних ймовірностей візьмемо долі голосів виборців, подані за відповідних кандидатів. Остаточний результат буде таким

Svoboda = S =

 = - 0.59 log₂(0.59) - 0.23 log₂(0.23) - 0.05 log₂(0.05) - 0.04 log₂(0.04) - 0.02 log₂(0.02) –

 0.06 log₂(0.06) - 0.04 log₂(0.04) = 1.7.

Порівняння президентських виборів в Україні з аналогічними виборами у Китаї і Сполучених штатах явно на користь України Свобода політичного вибору в Україні у 1.7 разів вища, ніж свобода політичного вибору у флагмані світової демократії – Сполучених штатах Америки. У Китаї свобода політичного вибору взагалі дорівнює нулю. 

Національна асоціація дослідників Голодомору - геноциду українців | Публікація 26Національна асоціація дослідників Голодомору - геноциду українців | Публікація 15

Валерій Швець